How To Find The Y Intercept On A Parabola
listenit
Apr 02, 2025 · 5 min read
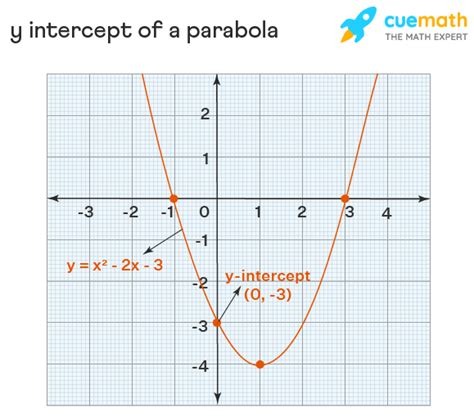
Table of Contents
How to Find the Y-Intercept on a Parabola
Finding the y-intercept of a parabola is a fundamental concept in algebra and precalculus. Understanding this allows you to accurately graph the parabola and analyze its key characteristics. This comprehensive guide will walk you through various methods, catering to different levels of mathematical understanding, ensuring you master this important skill. We'll cover parabolas in standard form, vertex form, and even explore how to find the y-intercept from a graph.
Understanding the Y-Intercept
Before diving into the methods, let's clarify what a y-intercept is. The y-intercept is the point where the parabola intersects the y-axis. Crucially, at this point, the x-coordinate is always zero. This simple fact forms the basis of all the methods we'll explore.
Method 1: Using the Standard Form of a Parabola
The standard form of a parabola's equation is given by:
y = ax² + bx + c
where 'a', 'b', and 'c' are constants. The beauty of this form lies in its direct revelation of the y-intercept.
Finding the Y-Intercept Directly from the Equation
The y-intercept occurs when x = 0. Substituting x = 0 into the standard form equation:
y = a(0)² + b(0) + c
This simplifies to:
y = c
Therefore, the y-intercept is simply the constant term 'c' in the standard form equation. This is the most straightforward method.
Example:
Consider the parabola y = 2x² - 5x + 3. Here, a = 2, b = -5, and c = 3. The y-intercept is (0, 3).
Method 2: Using the Vertex Form of a Parabola
The vertex form of a parabola's equation is:
y = a(x - h)² + k
where (h, k) represents the coordinates of the vertex. While not as immediately obvious as the standard form, we can still easily find the y-intercept using this form.
Finding the Y-Intercept from the Vertex Form
To find the y-intercept, we again substitute x = 0 into the equation:
y = a(0 - h)² + k
This simplifies to:
y = ah² + k
Therefore, the y-intercept is found by substituting x = 0 and calculating the resulting y-value.
Example:
Let's consider the parabola y = -1(x - 2)² + 4. Here, a = -1, h = 2, and k = 4. Substituting x = 0:
y = -1(0 - 2)² + 4 = -1(-2)² + 4 = -4 + 4 = 0
The y-intercept is (0, 0). This parabola intersects the y-axis at the origin.
Method 3: Using Factoring (Standard Form)
If the quadratic equation is easily factorable, factoring can provide an alternative route to finding the y-intercept.
Factorization and the Y-Intercept
Let's assume the parabola is represented as y = (x - r₁)(x - r₂). This is the factored form, where r₁ and r₂ are the x-intercepts (or roots). While this primarily reveals the x-intercepts, it implicitly contains the information for the y-intercept. To find the y-intercept, substitute x = 0:
y = (0 - r₁)(0 - r₂) = r₁r₂
Therefore, the y-intercept is (0, r₁r₂). Note that this method only works effectively if the quadratic equation is easily factored.
Example:
Consider the parabola y = x² - 5x + 6. This factors to y = (x - 2)(x - 3). The y-intercept is (0, (2)(3)) = (0, 6).
Method 4: Completing the Square (Standard to Vertex Form)
Completing the square transforms the standard form into the vertex form, offering another path to the y-intercept. This is particularly useful if factoring isn't straightforward.
Completing the Square and Finding the Y-Intercept
Let's walk through this process step-by-step, using an example.
Consider the equation y = x² + 6x + 5.
-
Group the x terms: y = (x² + 6x) + 5
-
Complete the square: To complete the square, take half of the coefficient of x (which is 6), square it ((6/2)² = 9), and add and subtract this value inside the parenthesis: y = (x² + 6x + 9 - 9) + 5
-
Factor the perfect square trinomial: y = (x + 3)² - 9 + 5
-
Simplify: y = (x + 3)² - 4
Now we have the vertex form: y = (x - (-3))² + (-4). The vertex is at (-3, -4). To find the y-intercept, substitute x = 0:
y = (0 + 3)² - 4 = 9 - 4 = 5
The y-intercept is (0, 5).
Method 5: Graphing and Identifying the Y-Intercept
Graphical representation offers a visual method for determining the y-intercept.
Visual Identification from the Graph
Plotting points or using graphing software, we can plot the parabola. The y-intercept is the point where the parabola crosses the y-axis. Simply read the y-coordinate at the point of intersection. This method is most useful for quick visual estimation or checking your calculations done using algebraic methods. However, it relies on the accuracy of your graph.
Common Mistakes to Avoid
- Confusing the y-intercept with the vertex: The y-intercept and the vertex are distinct points on the parabola. The y-intercept always has an x-coordinate of 0, whereas the vertex's x-coordinate is found using -b/(2a) for the standard form.
- Incorrectly substituting x = 0: Ensure you accurately substitute x = 0 into the parabola's equation. Even a simple arithmetic error will lead to an incorrect y-intercept.
- Forgetting to simplify: After substituting x = 0, always simplify your equation to find the y-coordinate of the y-intercept.
Advanced Applications and Extensions
Understanding the y-intercept is crucial for more advanced applications like:
- Analyzing the behavior of the parabola: The y-intercept gives initial insights into the parabola's overall shape and position.
- Solving real-world problems: Parabolas are frequently used to model various phenomena like projectile motion, where the y-intercept often represents the initial height.
- Working with transformations of parabolas: Understanding the y-intercept helps visualize how transformations affect the parabola's position and shape.
Conclusion
Finding the y-intercept of a parabola is a skill that underpins a deeper understanding of quadratic functions. This guide has provided multiple approaches – direct substitution in standard form, calculation from the vertex form, factoring, completing the square, and graphical identification – equipping you with versatile techniques to tackle various situations. Mastering these methods not only strengthens your algebraic skills but also enhances your problem-solving abilities in various mathematical and real-world contexts. Remember to practice regularly to reinforce your understanding and build confidence in identifying y-intercepts accurately.
Latest Posts
Latest Posts
-
What Percent Is 13 Of 16
Apr 03, 2025
-
What Is The Charge On A Potassium Ion
Apr 03, 2025
-
What Is The Symbol For Entropy
Apr 03, 2025
-
6 Less Than The Product Of 4 And X
Apr 03, 2025
-
What Planet Is The Closest Size To Earth
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Y Intercept On A Parabola . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
