How To Find The Volume Of A Hexagonal Prism
listenit
Mar 31, 2025 · 5 min read
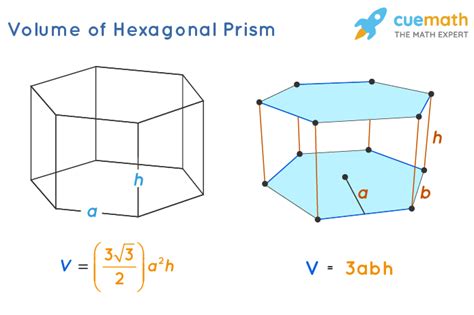
Table of Contents
How to Find the Volume of a Hexagonal Prism: A Comprehensive Guide
Finding the volume of a hexagonal prism might seem daunting at first, but with a structured approach and a clear understanding of the underlying principles, it becomes a straightforward calculation. This comprehensive guide will walk you through the process step-by-step, equipping you with the knowledge and tools to confidently tackle this geometrical challenge. We'll cover different methods, handle potential complexities, and provide practical examples to solidify your understanding.
Understanding the Hexagonal Prism
Before delving into the calculations, let's establish a firm grasp of what a hexagonal prism is. A hexagonal prism is a three-dimensional shape with two parallel hexagonal bases connected by six rectangular faces. Imagine a hexagonal column – that's essentially a hexagonal prism. The key features to understand are:
- Hexagonal Base: The two identical hexagonal faces at the top and bottom of the prism.
- Rectangular Faces: The six rectangular faces connecting the two hexagonal bases.
- Height (h): The perpendicular distance between the two hexagonal bases.
- Side Length (s): The length of each side of the hexagonal base.
- Apothem (a): The distance from the center of the hexagon to the midpoint of any side.
Method 1: Using the Area of the Hexagonal Base
This is the most common and arguably the easiest method to calculate the volume of a hexagonal prism. The formula relies on the fundamental principle that the volume of any prism is the product of its base area and its height.
Step 1: Calculate the Area of the Hexagonal Base
The area of a regular hexagon (a hexagon with all sides and angles equal) can be calculated using the following formula:
Area of Hexagon = (3√3/2) * s²
Where 's' represents the side length of the hexagon.
This formula might seem complicated at first, but it's simply a mathematical derivation of the hexagon's area based on its geometry. You can also break the hexagon into six equilateral triangles and calculate the area of one triangle then multiply it by 6. Remember, the area of an equilateral triangle is (√3/4) * s².
Step 2: Calculate the Volume
Once you've determined the area of the hexagonal base, calculating the volume is a simple multiplication:
Volume of Hexagonal Prism = Area of Hexagon * Height (h)
Therefore, combining the two steps, the complete formula becomes:
Volume = [(3√3/2) * s²] * h
Example:
Let's say we have a hexagonal prism with a side length (s) of 5 cm and a height (h) of 10 cm.
-
Area of Hexagon: (3√3/2) * 5² = (3√3/2) * 25 ≈ 64.95 cm²
-
Volume of Hexagonal Prism: 64.95 cm² * 10 cm = 649.5 cm³
Therefore, the volume of the hexagonal prism is approximately 649.5 cubic centimeters.
Method 2: Using the Apothem
The apothem (a) offers an alternative approach to calculating the area of the hexagonal base. The apothem is particularly useful when the side length isn't readily available.
Step 1: Calculate the Area of the Hexagonal Base (using apothem)
The area of a regular hexagon can also be calculated using the apothem:
Area of Hexagon = (1/2) * Perimeter * Apothem = (1/2) * 6s * a = 3sa
Where 's' is the side length and 'a' is the apothem.
Step 2: Calculate the Volume
The volume calculation remains the same as in Method 1:
Volume of Hexagonal Prism = Area of Hexagon * Height (h)
Therefore, combining the two steps, the complete formula becomes:
Volume = 3sa * h
Example:
Imagine a hexagonal prism with an apothem (a) of 4.33 cm, a side length (s) of 5 cm, and a height (h) of 10 cm.
-
Area of Hexagon: 3 * 5 cm * 4.33 cm = 64.95 cm²
-
Volume of Hexagonal Prism: 64.95 cm² * 10 cm = 649.5 cm³
The volume, using the apothem, is also approximately 649.5 cubic centimeters. This demonstrates the equivalence of both methods.
Handling Irregular Hexagonal Prisms
The formulas above apply specifically to regular hexagonal prisms. If you're dealing with an irregular hexagonal prism (where sides and angles are not all equal), the calculations become significantly more complex. There's no single, simple formula. You would need to:
-
Divide the irregular hexagon into smaller, simpler shapes: This might involve triangles, rectangles, or other polygons whose areas are easier to calculate.
-
Calculate the area of each smaller shape individually: Use appropriate formulas for each shape (e.g., triangle area = (1/2) * base * height, rectangle area = length * width).
-
Sum the areas of all smaller shapes: This will give you the total area of the irregular hexagonal base.
-
Multiply the total area by the height: This final step remains the same as for regular prisms. Volume = Base Area * Height
Practical Applications and Real-World Examples
Understanding how to calculate the volume of a hexagonal prism has numerous practical applications across various fields:
-
Architecture and Construction: Determining the volume of hexagonal pillars, columns, or structural elements in building design.
-
Engineering: Calculating the volume of hexagonal components in machinery, infrastructure, or manufacturing processes.
-
Packaging and Logistics: Optimizing the design and space utilization of hexagonal-shaped packaging.
-
Geology and Mining: Estimating the volume of hexagonal crystals or formations found in geological surveys.
Troubleshooting and Common Mistakes
-
Units: Always ensure consistent units throughout your calculations (e.g., all measurements in centimeters or all in meters). Mixing units will lead to incorrect results.
-
Regular vs. Irregular: Clearly identify whether the prism is regular or irregular. Use the appropriate method.
-
Apothem Calculation: If using the apothem method, ensure you have the correct apothem value. An inaccurate apothem will lead to an inaccurate volume calculation.
-
Significant Figures: Pay attention to significant figures in your measurements and calculations to maintain accuracy in your final answer.
Conclusion
Calculating the volume of a hexagonal prism, whether regular or irregular, is a fundamental skill in various fields. By understanding the underlying principles and applying the appropriate formulas, you can confidently tackle these calculations. Remember to meticulously check your measurements, maintain consistent units, and choose the correct method based on the characteristics of the hexagonal prism. With practice and attention to detail, you will master this important geometrical concept.
Latest Posts
Latest Posts
-
What Is Square Root Of 63
Apr 01, 2025
-
Least Common Multiple 2 And 4
Apr 01, 2025
-
How Does Igneous Rock Become Metamorphic
Apr 01, 2025
-
How Does Friction Affect The Motion Of Objects
Apr 01, 2025
-
Sr Oh 2 Strong Or Weak
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Volume Of A Hexagonal Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
