How To Find The Perpendicular Slope
listenit
Mar 28, 2025 · 5 min read
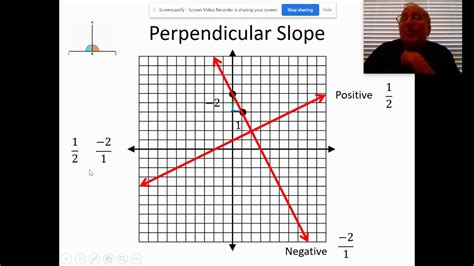
Table of Contents
How to Find the Perpendicular Slope: A Comprehensive Guide
Finding the perpendicular slope is a fundamental concept in geometry and algebra, crucial for understanding lines, their intersections, and various applications in fields like engineering and computer graphics. This comprehensive guide will walk you through the process of finding the perpendicular slope, clarifying the underlying principles and providing practical examples to solidify your understanding. We'll explore different approaches and address common challenges faced by students.
Understanding Slope and its Relationship with Perpendicular Lines
Before diving into finding the perpendicular slope, let's refresh our understanding of slope itself. The slope of a line represents its steepness or incline. It's defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. Mathematically, the slope (often denoted as m) is calculated as:
m = (y₂ - y₁) / (x₂ - x₁)
where (x₁, y₁) and (x₂, y₂) are any two points on the line.
Now, consider two perpendicular lines. Perpendicular lines intersect at a right angle (90°). The relationship between their slopes is key to understanding their perpendicularity: the slopes of perpendicular lines are negative reciprocals of each other.
Calculating the Perpendicular Slope: The Core Method
The core method for finding the perpendicular slope involves two simple steps:
-
Find the slope of the original line: This is done using the slope formula mentioned above. If the equation of the line is given in slope-intercept form (y = mx + b), the slope m is readily available as the coefficient of x.
-
Take the negative reciprocal: Once you have the slope of the original line, find its negative reciprocal. To do this:
- Change the sign: If the slope is positive, make it negative; if it's negative, make it positive.
- Invert the fraction: Flip the numerator and the denominator. If the slope is a whole number, consider it as a fraction with a denominator of 1 (e.g., 3 becomes 3/1).
Let's illustrate with an example:
Example 1: Find the perpendicular slope of a line with a slope of 2/3.
-
Original slope: m = 2/3
-
Negative reciprocal: -3/2
Therefore, the perpendicular slope is -3/2.
Example 2: Find the perpendicular slope of a line with a slope of -5.
-
Original slope: m = -5 (or -5/1)
-
Negative reciprocal: 1/5
Therefore, the perpendicular slope is 1/5.
Example 3: Find the perpendicular slope of a line passing through points (1, 2) and (4, 6).
-
Find the slope of the original line:
m = (6 - 2) / (4 - 1) = 4/3
-
Negative reciprocal: -3/4
Therefore, the perpendicular slope is -3/4.
Handling Special Cases: Horizontal and Vertical Lines
Horizontal and vertical lines represent special cases when dealing with perpendicular slopes:
-
Horizontal Line: A horizontal line has a slope of 0. Its perpendicular line is a vertical line, which has an undefined slope (because the denominator in the slope formula becomes zero).
-
Vertical Line: A vertical line has an undefined slope. Its perpendicular line is a horizontal line with a slope of 0.
Finding the Equation of a Perpendicular Line
Knowing the perpendicular slope is often a crucial step in finding the equation of a line perpendicular to a given line. You'll need a point on the perpendicular line to fully define its equation. This is typically done using the point-slope form of a linear equation:
y - y₁ = m(x - x₁)
where (x₁, y₁) is a point on the line, and m is the slope of the line.
Example 4: Find the equation of the line perpendicular to the line y = 2x + 1 and passing through the point (2, 3).
-
Slope of the original line: m = 2
-
Perpendicular slope: m⊥ = -1/2
-
Equation of the perpendicular line (using point-slope form):
y - 3 = -1/2(x - 2)
Simplifying, we get: y = -1/2x + 4
Applications of Perpendicular Slopes
Understanding perpendicular slopes has numerous applications across various fields:
-
Geometry: Constructing perpendicular bisectors, finding altitudes of triangles, determining if lines are perpendicular.
-
Computer Graphics: Creating right angles in designs and simulations.
-
Engineering: Designing structures with perpendicular supports for stability.
-
Physics: Analyzing motion and forces involving perpendicular vectors.
-
Calculus: Finding tangent and normal lines (which are perpendicular to each other).
Advanced Techniques and Considerations
While the core method effectively handles most scenarios, certain situations might require more advanced techniques:
Dealing with Lines in Standard Form
If the equation of the line is given in standard form (Ax + By = C), you'll first need to convert it to slope-intercept form (y = mx + b) to identify the slope. This involves solving the equation for y.
Using Vectors
Vectors provide an alternative approach to understanding perpendicularity. Two vectors are perpendicular if their dot product is zero. This method can be particularly useful in higher-dimensional spaces.
Applications in 3D Space
The concept of perpendicularity extends to three-dimensional space. Finding perpendicular slopes involves dealing with vectors and planes, requiring a deeper understanding of linear algebra.
Common Mistakes and How to Avoid Them
Several common mistakes can arise when calculating perpendicular slopes:
-
Forgetting the negative sign: Remember that the perpendicular slope is the negative reciprocal. Omitting the negative sign is a frequent error.
-
Incorrectly inverting the fraction: Ensure you correctly flip the numerator and denominator when finding the reciprocal.
-
Misinterpreting the slope from the equation: If the equation is not in slope-intercept form, carefully convert it before extracting the slope.
-
Confusing parallel and perpendicular lines: Remember that parallel lines have the same slope, while perpendicular lines have negative reciprocal slopes.
Conclusion
Finding the perpendicular slope is a fundamental skill with widespread applications. By mastering the core method, understanding special cases, and being aware of common pitfalls, you'll gain a solid grasp of this important concept. Remember to practice regularly to build your proficiency and confidence in applying this knowledge to various problems across different fields. Through consistent practice and a thorough understanding of the underlying principles, you can confidently tackle any problem involving perpendicular slopes. The applications of this skill are vast and valuable across numerous disciplines, making it a fundamental concept worth mastering.
Latest Posts
Latest Posts
-
What Is 6 To The Zeroth Power
Mar 31, 2025
-
Which Intermolecular Force Is The Weakest
Mar 31, 2025
-
How To Calculate Molar Mass Of A Gas
Mar 31, 2025
-
The Weaker The Acid The Stronger The Conjugate Base
Mar 31, 2025
-
How Many Neutrons Does Barium Have
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Perpendicular Slope . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
