How To Find The Perimeter Of A Right Angle Triangle
listenit
Apr 05, 2025 · 6 min read
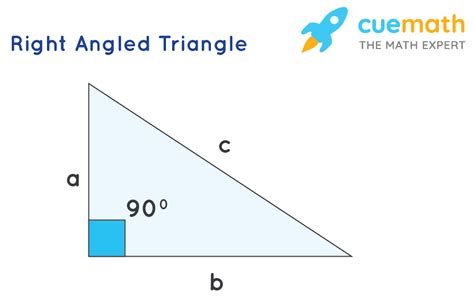
Table of Contents
How to Find the Perimeter of a Right-Angled Triangle: A Comprehensive Guide
Finding the perimeter of any triangle, including a right-angled triangle, is a fundamental concept in geometry. Understanding how to calculate this is crucial for various applications, from basic construction to advanced engineering. This comprehensive guide will walk you through different methods of calculating the perimeter of a right-angled triangle, exploring various scenarios and providing practical examples.
Understanding the Basics: Perimeter and Right-Angled Triangles
Before diving into the calculations, let's refresh our understanding of key terms.
Perimeter: The perimeter of any polygon (a closed shape with straight sides) is simply the total distance around its outer edges. For a triangle, this means adding the lengths of all three sides.
Right-Angled Triangle: A right-angled triangle is a special type of triangle where one of its angles measures exactly 90 degrees (a right angle). The side opposite the right angle is called the hypotenuse, and the other two sides are called legs or cathetus.
Method 1: Using the Pythagorean Theorem (When Sides are Known)
This is the most straightforward method when you already know the lengths of two sides of the right-angled triangle. The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Mathematically, it's represented as:
a² + b² = c²
Where:
- a and b are the lengths of the two legs.
- c is the length of the hypotenuse.
Once you've calculated the length of the hypotenuse using the Pythagorean theorem, you can easily find the perimeter by adding the lengths of all three sides:
Perimeter = a + b + c
Example:
Let's say a right-angled triangle has legs of length 3 cm and 4 cm. To find the hypotenuse:
- 3² + 4² = c²
- 9 + 16 = c²
- 25 = c²
- c = √25 = 5 cm
Therefore, the perimeter is 3 cm + 4 cm + 5 cm = 12 cm.
Method 2: Using Trigonometry (When One Side and One Angle are Known)
If you know the length of one side and the measure of one of the acute angles (angles other than the right angle), you can use trigonometry to find the lengths of the other two sides. The trigonometric functions sine (sin), cosine (cos), and tangent (tan) are essential here.
Let's assume you know the length of one leg (a) and the measure of the angle opposite to it (A):
- sin(A) = opposite/hypotenuse = a/c This allows you to calculate the hypotenuse (c).
- tan(A) = opposite/adjacent = a/b This allows you to calculate the other leg (b).
Once you've found the lengths of all three sides (a, b, and c), you can calculate the perimeter as before:
Perimeter = a + b + c
Example:
Suppose you have a right-angled triangle with one leg (a) measuring 6 cm and the angle opposite to it (A) measuring 30 degrees.
-
sin(30°) = 6/c
-
c = 6/sin(30°) = 6 / 0.5 = 12 cm
-
tan(30°) = 6/b
-
b = 6/tan(30°) = 6 / (1/√3) ≈ 10.39 cm
Therefore, the approximate perimeter is 6 cm + 10.39 cm + 12 cm ≈ 28.39 cm. Remember that trigonometric calculations often involve approximations depending on the precision of your calculator or software.
Method 3: Using Area and One Side (A Less Common Approach)
While less direct, you can determine the perimeter if you know the area (Area) of the right-angled triangle and the length of one of its legs (a).
The area of a right-angled triangle is given by:
Area = (1/2) * a * b
From this equation, you can find the length of the other leg (b):
b = (2 * Area) / a
Once you know both legs (a and b), you can use the Pythagorean theorem (as in Method 1) to calculate the hypotenuse (c) and then the perimeter.
Example:
Let's say the area of a right-angled triangle is 24 cm² and one leg (a) is 6 cm.
- b = (2 * 24 cm²) / 6 cm = 8 cm
- Now use the Pythagorean theorem: 6² + 8² = c² => c = 10 cm
- Perimeter = 6 cm + 8 cm + 10 cm = 24 cm
Solving Real-World Problems Involving Right-Angled Triangle Perimeters
The ability to calculate the perimeter of a right-angled triangle is vital in numerous practical scenarios. Here are a few examples:
1. Construction and Engineering: Determining the amount of material needed for a triangular structure, such as a roof truss or a support beam, necessitates accurate perimeter calculations.
2. Land Surveying: Right-angled triangles are frequently used in surveying to determine distances and boundaries. Calculating the perimeter of a triangular plot of land is crucial for accurate measurements and property assessments.
3. Navigation: In navigation, particularly maritime or aerial navigation, determining distances using right-angled triangles is common. Knowing the perimeter can help in planning routes and calculating travel times.
4. Computer Graphics and Game Development: Right-angled triangles form the basis of many shapes and objects in computer graphics and game development. Precise perimeter calculations are necessary for rendering objects accurately and realistically.
5. Physics and Engineering: Many physics problems involve the use of right-angled triangles, such as those concerning forces, velocities, and projectile motion. Calculating perimeters can be a part of solving these problems.
Advanced Concepts and Considerations
While the methods described above cover the most common scenarios, there are some additional factors to consider:
-
Units: Always ensure consistency in units throughout your calculations. If your measurements are in centimeters, your final answer should also be in centimeters.
-
Approximations: When using trigonometry or dealing with irrational numbers (such as the square root of non-perfect squares), remember that your final answer will be an approximation. The level of precision depends on the context and the required accuracy.
-
Complex Triangles: For more complex scenarios involving multiple triangles or triangles within other shapes, breaking down the problem into smaller, manageable right-angled triangles is a useful strategy.
Conclusion: Mastering Right-Angled Triangle Perimeter Calculations
Understanding how to calculate the perimeter of a right-angled triangle is a fundamental skill with wide-ranging applications. Whether you are a student tackling geometry problems, an engineer designing structures, or someone involved in a field requiring spatial reasoning, mastering these calculation methods will enhance your problem-solving capabilities. By utilizing the appropriate methods based on the given information, you can accurately and efficiently determine the perimeter of any right-angled triangle you encounter. Remember to practice regularly and check your work carefully to build confidence and accuracy.
Latest Posts
Latest Posts
-
How To Find Where The Tangent Line Is Horizontal
Apr 05, 2025
-
Arcsin 1 2 In Terms Of Pi
Apr 05, 2025
-
Is Salt A Compound Element Or Mixture
Apr 05, 2025
-
Is Potassium Iodide Covalent Or Ionic
Apr 05, 2025
-
Common Denominator Of 3 4 5
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Perimeter Of A Right Angle Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
