Arcsin 1 2 In Terms Of Pi
listenit
Apr 05, 2025 · 6 min read
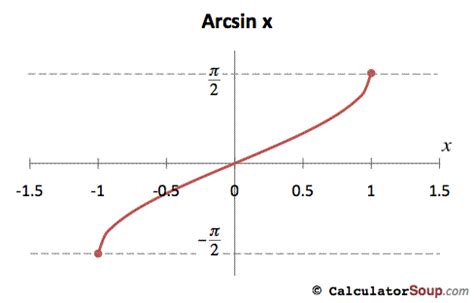
Table of Contents
Arcsin(1/2): Unveiling the Relationship with Pi
The inverse trigonometric functions, often denoted as arcsin, arccos, and arctan, play a crucial role in various mathematical and scientific fields. Understanding their properties, particularly their relationship with fundamental constants like π (pi), is essential for solving complex problems and gaining a deeper appreciation for their underlying nature. This article delves into the specific case of arcsin(1/2), exploring its connection to π and demonstrating its applications in various contexts.
Understanding the Arcsine Function
Before we delve into the specific case of arcsin(1/2), let's establish a foundational understanding of the arcsine function itself. The arcsine function, denoted as arcsin(x) or sin⁻¹(x), is the inverse function of the sine function. In simpler terms, it answers the question: "What angle has a sine value of x?"
Key Characteristics of Arcsin(x):
-
Domain: The domain of arcsin(x) is restricted to the interval [-1, 1]. This is because the sine function's range is [-1, 1], and the inverse function's domain is the range of the original function. Values outside this range yield undefined results.
-
Range: The range of arcsin(x) is [-π/2, π/2], or -90° to 90° in degrees. This restricted range ensures that the arcsine function is a one-to-one function, meaning each input has only one output. This restriction is crucial for defining a proper inverse function.
-
Principal Value: The principal value of arcsin(x) is the value within the range [-π/2, π/2]. This ensures consistency and avoids ambiguity when dealing with multiple possible angles that have the same sine value.
Solving Arcsin(1/2)
Now, let's focus on the specific problem at hand: finding the value of arcsin(1/2). This involves determining the angle whose sine is equal to 1/2.
We know that the sine function represents the ratio of the opposite side to the hypotenuse in a right-angled triangle. Therefore, we are looking for an angle where the opposite side is half the length of the hypotenuse.
A common right-angled triangle that satisfies this condition is a 30-60-90 triangle. In this triangle, the ratio of the sides is 1:√3:2. The sine of the 30° angle (or π/6 radians) is indeed 1/2.
Therefore:
arcsin(1/2) = π/6
This is the principal value of arcsin(1/2) because it falls within the range [-π/2, π/2].
Exploring Other Potential Solutions
While π/6 is the principal value, it's crucial to remember that the sine function is periodic. This means that it repeats its values at regular intervals. Consequently, there are infinitely many angles that have a sine value of 1/2.
To find these other solutions, we can use the general solution for sine functions:
x = nπ + (-1)^n * α
Where:
- 'n' is an integer (0, ±1, ±2, ±3, ...)
- 'α' is the principal value (π/6 in our case)
Using this formula, we can generate other angles with a sine of 1/2:
- n = 0: 0π + (-1)^0 * (π/6) = π/6
- n = 1: 1π + (-1)^1 * (π/6) = 5π/6
- n = 2: 2π + (-1)^2 * (π/6) = 13π/6
- n = -1: -1π + (-1)^-1 * (π/6) = -7π/6
- n = -2: -2π + (-1)^-2 * (π/6) = -11π/6
And so on... These angles all have a sine value of 1/2, but only π/6 falls within the principal range of arcsin(x).
Applications of Arcsin(1/2) in Various Fields
The knowledge of arcsin(1/2) and its relationship with π has significant applications across diverse fields:
1. Trigonometry and Geometry:
- Solving Triangles: In solving triangles, arcsin(1/2) is frequently encountered when determining angles based on known side lengths.
- Circular Motion: Arcsin(1/2) plays a role in analyzing circular motion and oscillatory systems.
2. Physics:
- Oscillatory Systems: Many physical phenomena, like simple harmonic motion (pendulums, springs), involve sinusoidal functions. Determining the phase or angular position often requires using arcsin(1/2) or similar inverse trigonometric functions.
- Wave Phenomena: Analyzing wave properties (like amplitude and phase) frequently employs inverse trigonometric functions.
3. Engineering:
- Signal Processing: Inverse trigonometric functions are crucial in processing and analyzing signals, which often have sinusoidal components.
- Control Systems: In designing control systems, inverse trigonometric functions aid in analyzing system behavior and stability.
4. Computer Graphics and Game Development:
- Rotation and Transformations: Inverse trigonometric functions are integral to manipulating objects and defining transformations within three-dimensional spaces.
5. Calculus:
- Integration and Differentiation: Arcsin(x) itself is a crucial function in integral calculus, and its derivatives are frequently used in solving complex problems.
Illustrative Example: Simple Harmonic Motion
Let's consider a simple example to demonstrate the application of arcsin(1/2) in a physical scenario. Imagine a simple pendulum swinging back and forth. The displacement of the pendulum bob from its equilibrium position can be described using a sinusoidal function:
x(t) = A * sin(ωt + φ)
Where:
- x(t) is the displacement at time 't'
- A is the amplitude (maximum displacement)
- ω is the angular frequency
- φ is the phase angle
Let's say that at a specific time t₁, the displacement x(t₁) is half the amplitude (x(t₁) = A/2). To find the phase angle φ at this time, we would use the following equation:
sin(ωt₁ + φ) = 1/2
Solving for φ:
ωt₁ + φ = arcsin(1/2) = π/6
This shows how arcsin(1/2) directly helps in determining the phase angle of an oscillatory system at a particular point in time.
Advanced Concepts and Further Exploration
The relationship between arcsin(1/2) and π opens doors to further exploration of more advanced mathematical concepts. These include:
- Complex Numbers: Extending the arcsine function to the complex plane reveals interesting properties and connections to other mathematical domains.
- Series Expansions: The arcsine function can be represented using Taylor series or other infinite series expansions, which are valuable tools in approximation and numerical analysis.
- Differential Equations: The arcsine function and its derivatives frequently appear in the solutions of differential equations, which model many physical and engineering systems.
Conclusion: The Significance of Arcsin(1/2) and Pi
The seemingly simple equation arcsin(1/2) = π/6 holds profound significance in mathematics, science, and engineering. Its connection to π underscores the fundamental role of trigonometric functions and their inverse counterparts in describing periodic phenomena and solving geometrical problems. Understanding this relationship not only enhances our grasp of fundamental mathematical concepts but also equips us to effectively tackle a broad range of applications across multiple disciplines. From solving triangles to analyzing complex physical systems, the knowledge of arcsin(1/2) proves invaluable in numerous contexts. Further exploration of this relationship will undoubtedly continue to yield deeper insights and innovative applications in the years to come.
Latest Posts
Latest Posts
-
Three Structural Isomers Have The Formula C5h12
Apr 06, 2025
-
The Four Nitrogenous Bases Found In Dna Are
Apr 06, 2025
-
Why Is Water Liquid At Room Temp
Apr 06, 2025
-
What Is The Lcm Of 6 And 16
Apr 06, 2025
-
A Gardener Is Mowing A 20 By 40 Yard
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Arcsin 1 2 In Terms Of Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
