How To Find Radius Of A Circle Given Circumference
listenit
Mar 28, 2025 · 5 min read
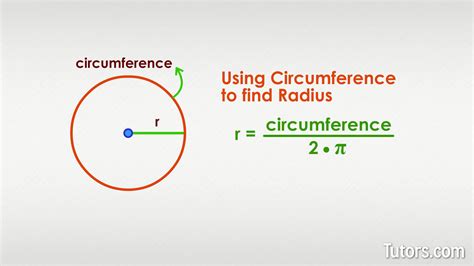
Table of Contents
How to Find the Radius of a Circle Given its Circumference
Determining the radius of a circle when you only know its circumference might seem like a complex mathematical problem, but it's surprisingly straightforward. This comprehensive guide will walk you through the process, explaining the underlying principles, providing step-by-step instructions, and offering practical examples to solidify your understanding. We'll also delve into related concepts and explore how this fundamental calculation finds application in various fields.
Understanding the Relationship Between Circumference and Radius
The foundation of solving this problem lies in the fundamental relationship between a circle's circumference (C) and its radius (r). The circumference, the distance around the circle, is directly proportional to the radius. This relationship is expressed by the following formula:
C = 2πr
Where:
- C represents the circumference of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter.
- r represents the radius of the circle.
This formula encapsulates the core principle: the circumference is always a constant multiple (2π) of the radius. This constant relationship allows us to determine the radius if we know the circumference, and vice versa.
Step-by-Step Guide to Calculating the Radius
Now let's break down the process of finding the radius (r) given the circumference (C) into simple, manageable steps:
Step 1: Write Down the Formula
Begin by writing down the fundamental formula that connects circumference and radius:
C = 2πr
Step 2: Substitute the Known Value (Circumference)
Substitute the given value of the circumference (C) into the formula. Let's assume, for example, that the circumference of the circle is 25 centimeters. The equation now becomes:
25 cm = 2πr
Step 3: Isolate the Radius (r)
Our goal is to solve for 'r', the radius. To do this, we need to isolate 'r' on one side of the equation. We can achieve this by performing algebraic manipulations. First, divide both sides of the equation by 2π:
r = 25 cm / 2π
Step 4: Calculate the Radius
Now, it's time to perform the calculation. Remember to use an accurate value for π (pi). Using a calculator with a π function provides the most precise result. For our example:
r ≈ 25 cm / (2 * 3.14159)
r ≈ 25 cm / 6.28318
r ≈ 3.98 cm
Therefore, the radius of the circle with a circumference of 25 centimeters is approximately 3.98 centimeters.
Practical Applications and Real-World Examples
The ability to calculate the radius from the circumference is crucial in numerous fields and everyday scenarios:
-
Engineering and Design: Engineers use this calculation extensively in designing circular components for machinery, infrastructure projects, and various other applications. Determining the radius is essential for ensuring proper dimensions and functionality.
-
Construction: From laying out circular foundations to building circular structures, understanding this relationship is critical for precise measurements and efficient construction.
-
Cartography and Geography: In mapping and geographical studies, the ability to determine the radius of a circle (e.g., a region of influence around a geographical feature) based on its circumference is frequently employed.
-
Manufacturing: The manufacturing industry utilizes these calculations in designing and producing circular parts, packaging, and other items requiring precise dimensions.
-
Astronomy: In astronomy, the calculation finds use in determining the size of celestial objects based on observed circumferences or distances.
Advanced Concepts and Related Calculations
Let's explore some related concepts and calculations that build upon the fundamental relationship between circumference and radius:
-
Diameter: The diameter (d) of a circle is twice its radius. Therefore, once you have calculated the radius, you can easily find the diameter using the formula: d = 2r
-
Area: The area (A) of a circle is calculated using the formula: A = πr². Once you have determined the radius, you can calculate the area of the circle. This is particularly useful in various fields where determining the area of circular regions is important.
-
Arc Length: If you know a portion of the circumference (the arc length), you can determine the radius if you also know the central angle subtended by that arc. The formula for arc length is: Arc Length = rθ, where θ is the angle in radians.
-
Sector Area: Similarly, if you know the area of a sector of a circle and the central angle of that sector, you can calculate the radius. The formula for the area of a sector is: Sector Area = (1/2)r²θ.
-
Circumference Calculation with Error Analysis: In real-world scenarios, the measured circumference might have associated errors. Understanding how these errors propagate to the radius calculation is crucial for accurate results. This involves considering the uncertainty in the circumference measurement and applying principles of error propagation to estimate the uncertainty in the calculated radius.
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when calculating the radius from the circumference:
-
Incorrect Value of π: Using an inaccurate approximation of π can lead to significant errors in the final result. Use a calculator with a π function or a sufficiently accurate approximation (at least 3.14159).
-
Algebraic Errors: Ensure you are performing the algebraic manipulations correctly when isolating 'r' in the formula. Double-check your steps to avoid errors.
-
Unit Consistency: Maintain consistent units throughout your calculations. If the circumference is given in centimeters, the radius will also be in centimeters.
-
Calculator Errors: Carefully input the numbers into your calculator to avoid keying errors.
Conclusion
Finding the radius of a circle given its circumference is a fundamental concept in mathematics with extensive real-world applications. By understanding the core formula (C = 2πr) and following the step-by-step guide provided, you can confidently perform this calculation. Remember to use an accurate value for π and double-check your calculations to ensure accuracy. Mastering this skill opens doors to understanding more complex geometrical concepts and solving problems in various fields, from engineering and design to astronomy and beyond. Always strive for accuracy and understand the limitations of your measurements and calculations, especially when working with real-world data.
Latest Posts
Latest Posts
-
What Is 4 12 In Simplest Form
Mar 31, 2025
-
Is 5 16 Bigger Than 1 4
Mar 31, 2025
-
What Is The Fraction For 0 04
Mar 31, 2025
-
Replication Is Called A Semi Conservative Process Because
Mar 31, 2025
-
How Many Cups In One Half Gallon
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Find Radius Of A Circle Given Circumference . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
