Is 5 16 Bigger Than 1 4
listenit
Mar 31, 2025 · 5 min read
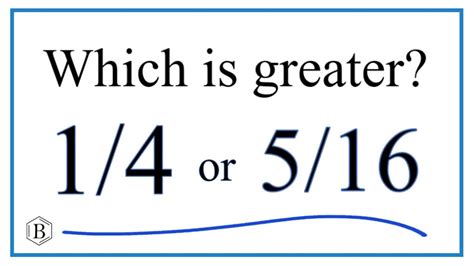
Table of Contents
Is 5/16 Bigger Than 1/4? A Deep Dive into Fraction Comparison
Are you struggling with comparing fractions? Determining whether 5/16 is bigger than 1/4 might seem simple at first glance, but understanding the underlying principles is crucial for mastering fractions. This comprehensive guide will not only answer the question definitively but also equip you with the tools and techniques to confidently compare any two fractions.
Understanding Fractions
Before tackling the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 5/16, 5 is the numerator and 16 is the denominator. This means we have 5 parts out of a total of 16 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most straightforward method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of their numerators.
Steps:
-
Find the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. For 16 and 4, the LCM is 16.
-
Convert each fraction to an equivalent fraction with the LCM as the denominator.
-
For 5/16, the denominator is already 16, so it remains unchanged.
-
For 1/4, we need to multiply both the numerator and the denominator by 4 to get a denominator of 16: (1 × 4) / (4 × 4) = 4/16.
-
-
Compare the numerators. Now that both fractions have the same denominator, we can directly compare their numerators: 5 > 4.
-
Conclusion: Since 5/16 (which is equal to 5/16) has a larger numerator than 4/16, we conclude that 5/16 is bigger than 1/4.
Method 2: Converting to Decimals
Another effective approach involves converting both fractions to decimals. This method is particularly useful when dealing with fractions that are difficult to compare using a common denominator.
Steps:
-
Divide the numerator by the denominator for each fraction.
- 5/16 = 0.3125
- 1/4 = 0.25
-
Compare the decimal values. 0.3125 > 0.25.
-
Conclusion: Because 0.3125 is greater than 0.25, we confirm that 5/16 is bigger than 1/4.
Method 3: Visual Representation
While not as precise as the previous methods, a visual approach can be helpful for understanding the relative sizes of fractions. Imagine two identical circles or rectangles.
Steps:
-
Divide the first shape into 16 equal parts. Shade 5 of these parts to represent 5/16.
-
Divide the second shape into 4 equal parts. Shade 1 of these parts to represent 1/4.
-
Compare the shaded areas. Visually, you'll observe that the shaded area representing 5/16 is larger than the shaded area representing 1/4.
-
Conclusion: This visual comparison reinforces the conclusion that 5/16 is bigger than 1/4.
Why Understanding Fraction Comparison is Crucial
The ability to compare fractions is fundamental to various aspects of mathematics and everyday life. Here's why it's essential:
-
Problem-solving: Many mathematical problems, especially in algebra and calculus, involve comparing fractions to determine inequalities or find solutions.
-
Data analysis: In statistics and data analysis, comparing fractions helps in interpreting data, making predictions, and drawing meaningful conclusions.
-
Real-world applications: From cooking and baking (measuring ingredients) to construction and engineering (measuring materials), comparing fractions is essential for accuracy and precision.
-
Financial literacy: Understanding fractions is crucial for managing finances, calculating interest rates, and making informed financial decisions.
Advanced Fraction Comparison Techniques
For more complex scenarios involving multiple fractions, more sophisticated techniques might be necessary:
-
Cross-multiplication: For comparing two fractions, a/b and c/d, cross-multiply: a × d and b × c. The fraction with the larger product of cross-multiplication is the larger fraction. This method avoids finding the LCM, especially helpful when dealing with larger numbers.
-
Converting to percentages: Converting fractions to percentages offers another perspective for comparison. This method is particularly useful when comparing fractions to percentages directly or when dealing with proportions.
-
Using a number line: Representing fractions on a number line provides a clear visual comparison of their relative positions. This method is particularly beneficial for visualizing the order of a series of fractions.
Common Mistakes to Avoid When Comparing Fractions
-
Comparing numerators directly without considering denominators: This is a common mistake leading to incorrect conclusions. Always ensure you have a common denominator or use a different method before comparing the numerators.
-
Incorrectly converting fractions to decimals: Rounding off decimal values too early can result in inaccuracies when comparing fractions. Maintain sufficient precision during the conversion process.
-
Misinterpreting visual representations: While visual aids are helpful, they might not always offer sufficient precision for complex fraction comparisons. Always rely on algebraic or numerical methods for accurate conclusions.
Practicing Fraction Comparison
Regular practice is crucial to master fraction comparison. Start with simple fractions and gradually move towards more complex ones. Use online resources, textbooks, or worksheets to find practice problems. The more you practice, the more confident and efficient you'll become in comparing fractions.
Conclusion: Mastering the Art of Fraction Comparison
Comparing fractions, while initially seeming challenging, becomes straightforward with the right techniques and practice. Understanding the fundamental concepts of numerators, denominators, and the methods discussed – finding a common denominator, converting to decimals, and using visual representations – will equip you to confidently tackle any fraction comparison problem. Remember to avoid common mistakes and practice regularly to build your mastery. With consistent effort, comparing fractions will become second nature, enhancing your mathematical skills and broadening your problem-solving capabilities. So, the next time you encounter a fraction comparison, approach it with confidence, knowing you have the tools to solve it accurately and efficiently. The simple question, "Is 5/16 bigger than 1/4?" becomes a stepping stone towards a deeper understanding of the fascinating world of fractions.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 32 And 36
Apr 01, 2025
-
Least Common Multiple Of 4 And 30
Apr 01, 2025
-
The Principle Of Probability Can Be Used To
Apr 01, 2025
-
Y Varies Jointly As X And Z
Apr 01, 2025
-
What Is The Si Base Unit For Time
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is 5 16 Bigger Than 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
