How To Find Mass Of Planet
listenit
Apr 01, 2025 · 7 min read
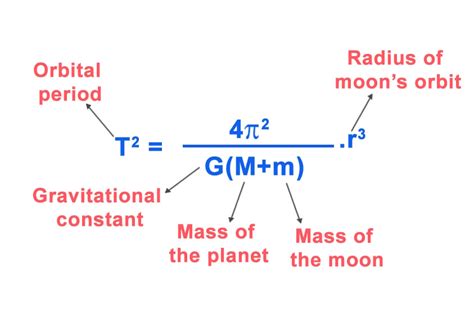
Table of Contents
How to Find the Mass of a Planet: A Comprehensive Guide
Determining the mass of a planet, a seemingly insurmountable task, is actually achievable through a variety of methods, each relying on different principles of physics and astronomical observation. This comprehensive guide will explore these methods, detailing the underlying science and the practical considerations involved in each approach. Understanding these techniques provides valuable insight into how we unravel the mysteries of our solar system and beyond.
Method 1: Using Kepler's Third Law and the Orbital Period of a Satellite
One of the most fundamental methods for determining a planet's mass leverages Kepler's Third Law of Planetary Motion. This law states that the square of the orbital period of a celestial body is directly proportional to the cube of the semi-major axis of its orbit. Mathematically, this is represented as:
T² ∝ a³
where:
- T is the orbital period of the satellite (the time it takes to complete one orbit around the planet).
- a is the semi-major axis of the satellite's orbit (the average distance between the satellite and the planet).
However, to determine the planet's mass, we need a more refined version of Kepler's Third Law, which incorporates the gravitational constant (G) and the combined mass of the planet (M<sub>p</sub>) and its satellite (M<sub>s</sub>):
(T²/4π²) = (a³/G(M<sub>p</sub> + M<sub>s</sub>))
Since the mass of the planet is significantly larger than the mass of its satellite (M<sub>p</sub> >> M<sub>s</sub>), we can simplify the equation to:
(T²/4π²) = (a³/GM<sub>p</sub>)
By observing the orbital period (T) and semi-major axis (a) of a satellite orbiting the planet, and knowing the gravitational constant (G = 6.674 x 10<sup>-11</sup> Nm²/kg²), we can solve for the planet's mass (M<sub>p</sub>). This method is particularly effective when dealing with planets possessing moons or artificial satellites.
Practical Considerations and Refinements:
- Accurate Measurements: The accuracy of this method hinges on precisely measuring the orbital period and semi-major axis. Sophisticated astronomical techniques, including radar ranging and precise astrometry, are crucial for achieving high accuracy. Errors in these measurements directly translate to errors in the calculated mass.
- Perturbations: The orbits of celestial bodies are not perfectly elliptical; they are subject to gravitational perturbations from other planets and celestial objects. These perturbations need to be accounted for to obtain a more accurate result. Advanced mathematical models incorporating these perturbations are used to refine the calculations.
- Non-Keplerian Orbits: Some satellites may have orbits that deviate significantly from Keplerian ellipses due to factors like atmospheric drag (for close-orbiting satellites) or non-uniform mass distribution within the planet. These situations require more complex calculations to accurately determine the planet's mass.
Method 2: Using the Gravitational Influence on Other Objects
Planets exert a gravitational influence on other celestial bodies, causing subtle changes in their orbits. By carefully observing these orbital perturbations, we can infer information about the planet's mass. This method is particularly useful for planets that lack readily observable satellites.
Applying Newton's Law of Universal Gravitation:
Newton's Law of Universal Gravitation states that the force of gravity between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between them:
F = G(M<sub>p</sub>M<sub>o</sub>)/r²
where:
- F is the gravitational force between the planet and another object.
- G is the gravitational constant.
- M<sub>p</sub> is the mass of the planet.
- M<sub>o</sub> is the mass of the other object.
- r is the distance between the centers of the planet and the other object.
By observing the orbital deviations of a nearby star or another planet caused by the gravitational pull of the target planet, we can estimate the force (F). Knowing the mass (M<sub>o</sub>) and distance (r) to the other object, we can then solve for the planet's mass (M<sub>p</sub>). This is a more complex method requiring precise astrometric observations and sophisticated computational models to analyze the data.
Practical Considerations:
- Sensitivity of Measurements: The gravitational influence of a planet on other objects is often small, requiring extremely precise astrometric measurements to detect and analyze. Advanced telescopes and sophisticated data analysis techniques are necessary.
- Multiple Body Interactions: The gravitational interactions between multiple bodies are complex and require careful consideration. The presence of other planets or stars can complicate the analysis, requiring sophisticated numerical simulations to separate the influence of the target planet from other factors.
- Data Acquisition Time: Observing subtle orbital perturbations requires long-term observational datasets, often spanning several years or even decades, to allow for the detection of significant changes in the orbits of other objects.
Method 3: Transit Timing Variations (TTV)
When a planet transits (passes in front of) its star, the slight dimming of the star's light can be measured. However, if the planet is affected by the gravitational pull of other planets, its transit timing will vary slightly from its predicted time. These Transit Timing Variations (TTV) can be used to estimate the masses of both the transiting planet and any perturbing planets.
This technique is based on the principles of Keplerian mechanics and relies on precise photometric measurements of the star's brightness during transits. By analyzing the deviations in the transit timings, researchers can infer the mass of the planet and other nearby planets affecting its orbit. This method is particularly useful for detecting exoplanets and estimating their masses.
Practical Considerations:
- High Precision Photometry: The success of this method depends on extremely precise photometric measurements of the star's brightness, requiring sophisticated telescopes and detectors.
- Data Analysis Complexity: Analyzing the TTV data requires sophisticated statistical and computational techniques to disentangle the effects of multiple planets on the transiting planet's orbit.
- Orbital Configurations: The effectiveness of the TTV method is highly dependent on the orbital configurations of the planets involved. Certain orbital configurations are more conducive to detecting and analyzing TTVs than others.
Method 4: Radial Velocity Method and Mass-Radius Relationship
The radial velocity method, also known as the Doppler spectroscopy method, is commonly used to detect exoplanets. By observing the slight wobble in a star's motion caused by an orbiting planet, the planet's minimum mass can be estimated. However, to obtain the true mass, we also need to know the inclination of the planet's orbit.
The inclination is the angle between the plane of the planet's orbit and the plane of the sky. If the orbit is edge-on (inclination of 90 degrees), the measured minimum mass is the true mass. However, if the orbit is not edge-on, the true mass will be larger than the minimum mass.
Combining radial velocity measurements with information about the planet's radius (obtained through transit observations), we can use a mass-radius relationship to estimate the planet's bulk density. This density provides constraints on the planet's composition and helps refine the mass estimation. This approach assumes certain physical models for the planet's interior structure.
Practical Considerations:
- Inclination Uncertainty: The main limitation of this method is the uncertainty associated with the orbital inclination, which can significantly impact the accuracy of the mass estimate.
- Atmospheric Effects: Atmospheric effects can influence the precision of radial velocity measurements, requiring careful calibration and correction.
- Stellar Activity: Stellar activity, such as starspots and flares, can mimic the signature of an orbiting planet and complicate the analysis.
Conclusion:
Determining the mass of a planet is a complex endeavor that often involves multiple techniques and careful consideration of various factors. The methods discussed here—using Kepler's Third Law, gravitational influence, transit timing variations, and the radial velocity method—each offer unique advantages and limitations depending on the specific circumstances and available data. The accuracy of the mass estimation ultimately depends on the precision of the measurements and the sophistication of the analytical methods employed. Advancements in astronomical observation techniques and data analysis continuously improve our ability to refine these methods and probe the masses of planets both within and beyond our solar system, deepening our understanding of planetary formation and evolution.
Latest Posts
Latest Posts
-
Most Reactive Group On The Periodic Table
Apr 02, 2025
-
How To Solve Multi Step Inequalities
Apr 02, 2025
-
Percent Composition Of Mg No3 2
Apr 02, 2025
-
How To Convert 3 8 Into A Decimal
Apr 02, 2025
-
Natural Resources Of The Northeast Region
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Find Mass Of Planet . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
