How Many Right Angles Can A Trapezoid Have
listenit
Apr 01, 2025 · 5 min read
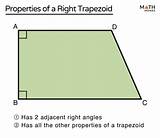
Table of Contents
How Many Right Angles Can a Trapezoid Have? A Comprehensive Exploration
The question of how many right angles a trapezoid can possess is a deceptively simple one that delves into the fascinating world of geometry and its fundamental shapes. While the immediate answer might seem obvious, a deeper understanding requires exploring the defining characteristics of trapezoids and their variations. This article will comprehensively examine the possibilities, addressing common misconceptions and solidifying your understanding of this quadrilateral.
Defining the Trapezoid: A Foundation for Understanding
Before we delve into the number of right angles, let's firmly establish what constitutes a trapezoid. A trapezoid, also known as a trapezium in some regions, is a quadrilateral—a four-sided polygon—defined by a single, crucial characteristic: it has at least one pair of parallel sides. These parallel sides are called bases, and the other two sides are called legs or lateral sides. Crucially, there's no restriction on the lengths of the sides or the angles between them, except for the parallelism of the bases.
This seemingly simple definition opens the door to a surprising variety of trapezoid shapes. This variability is key to understanding how many right angles a trapezoid can have.
Exploring the Possibilities: Right Angles in Trapezoids
The possibilities regarding right angles in trapezoids are more nuanced than a simple "one" or "two" answer. Let's explore the different scenarios:
1. Trapezoids with Exactly One Right Angle
It is entirely possible, and indeed quite common, to have a trapezoid with precisely one right angle. Imagine a rectangle that's been "sheared" or tilted slightly. One pair of opposite sides remain parallel, fulfilling the trapezoid definition, while one of the other angles is now acute, and the adjacent angle, obtuse. This configuration perfectly illustrates a trapezoid with only one right angle.
Key characteristics:
- One pair of parallel sides (bases): This is the fundamental requirement for any trapezoid.
- One 90-degree angle: This angle is formed where one of the legs meets a base.
- Other angles are not 90 degrees: The remaining angles will be either acute (less than 90 degrees) or obtuse (greater than 90 degrees), depending on the "tilt" of the trapezoid.
2. Trapezoids with Exactly Two Right Angles
This scenario is also possible. Consider a trapezoid where two adjacent angles are both 90 degrees. These right angles must be formed by the legs meeting the bases. The parallel sides ensure that the other two angles are supplementary (add up to 180 degrees), which is a characteristic of parallel lines intersected by a transversal.
Key characteristics:
- One pair of parallel sides (bases): This is always a defining characteristic.
- Two 90-degree angles: These angles are adjacent to each other and lie at the ends of a leg.
- Two supplementary angles: The remaining angles must add up to 180 degrees. This implies one is acute and the other obtuse.
This type of trapezoid is often referred to as a right trapezoid.
3. Trapezoids with Three or Four Right Angles
Can a trapezoid have three or four right angles? Let's examine:
-
Three right angles: If a trapezoid has three right angles, the fourth angle must also be 90 degrees to satisfy the sum of interior angles in a quadrilateral (360 degrees). But if all four angles are 90 degrees, the shape is actually a rectangle—a special case of a parallelogram and thus, a special case of a trapezoid. Therefore, a trapezoid cannot have exactly three right angles.
-
Four right angles: As mentioned above, a trapezoid with four right angles is a rectangle, a special type of trapezoid because it fulfills the minimum condition of having at least one pair of parallel sides. However, it's important to note that rectangles, squares (which are special rectangles), and other parallelograms are considered trapezoids because they meet the minimum condition.
Misconceptions and Clarifications
It's crucial to address some common misconceptions surrounding trapezoids and right angles:
-
Trapezoids must have only one pair of parallel sides: This is the defining characteristic. Any more or less parallel sides disqualifies it from being a trapezoid.
-
All trapezoids are irregular: This is incorrect. While many trapezoids are irregular (meaning sides and angles are of different lengths and measures), special types, such as right trapezoids and isosceles trapezoids, are perfectly valid and have specific characteristics.
-
A trapezoid cannot be a rectangle: Rectangles are a subset of trapezoids. They satisfy the condition of having at least one pair of parallel sides, which is the minimum requirement to be classified as a trapezoid.
Isosceles Trapezoids and Right Angles
An isosceles trapezoid is a special type of trapezoid where the legs (non-parallel sides) are equal in length. While an isosceles trapezoid can have two right angles (becoming a rectangle), it cannot have only one or three right angles. The symmetry inherent in an isosceles trapezoid ensures this limitation.
Real-World Applications: Why Understanding Trapezoids Matters
Understanding the properties of trapezoids, including the possibilities of right angles, isn't just an academic exercise. Trapezoids appear frequently in various real-world applications, such as:
-
Architecture and Construction: Trapezoidal shapes are often used in building designs, structural supports, and window designs.
-
Engineering: Trapezoidal structures can be found in bridges, dams, and other engineering projects.
-
Art and Design: The unique properties of trapezoids lend themselves to artistic compositions and design elements.
-
Everyday Objects: Many common objects, such as certain types of tables, picture frames, and traffic signs, utilize trapezoidal shapes.
Conclusion: A Deeper Dive into Trapezoidal Geometry
The seemingly simple question of how many right angles a trapezoid can have reveals a surprisingly rich understanding of geometric principles. While a trapezoid can have one or two right angles, it cannot have three. Four right angles defines a rectangle, which is a special case within the larger category of trapezoids. This exploration highlights the importance of understanding definitions, exploring variations, and appreciating the nuances within seemingly simple geometric concepts. A thorough understanding of trapezoidal properties is valuable in various disciplines, emphasizing the importance of geometric literacy in a wide range of fields. By solidifying your grasp of this fundamental shape, you build a stronger foundation for more advanced geometric explorations.
Latest Posts
Latest Posts
-
How Many Revolutions Are In A Radian
Apr 02, 2025
-
The Si Unit For Energy Is
Apr 02, 2025
-
Finding The Angle Between Two Planes
Apr 02, 2025
-
What Are The Common Multiples Of 2 And 7
Apr 02, 2025
-
Ratio Of Each 90 If Ratio Is 7 3
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many Right Angles Can A Trapezoid Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
