How Many Lines Of Symmetry In A Rectangle
listenit
Mar 27, 2025 · 6 min read
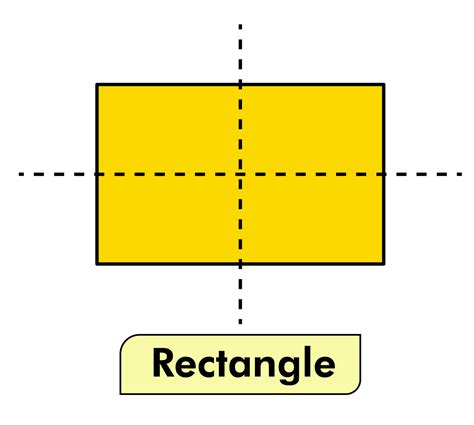
Table of Contents
How Many Lines of Symmetry Does a Rectangle Have? A Comprehensive Exploration
Symmetry, a fundamental concept in mathematics and geometry, describes the balanced distribution of a shape's features. Understanding symmetry is crucial in various fields, from art and design to engineering and physics. This article delves into the fascinating world of symmetry, focusing specifically on rectangles and the number of lines of symmetry they possess. We'll explore the definition of symmetry, different types of symmetry, and then meticulously examine the specific case of the rectangle.
Defining Symmetry and Lines of Symmetry
Before diving into the specifics of rectangular symmetry, let's establish a clear understanding of the core concepts. Symmetry, in its simplest form, means that a shape can be folded along a line (or rotated about a point) so that the two halves perfectly match each other. This line (or point) is known as a line of symmetry (or axis of symmetry) or a point of symmetry (or center of symmetry), respectively.
There are two primary types of symmetry relevant to our discussion:
1. Line Symmetry (Reflectional Symmetry)
Line symmetry, also called reflectional symmetry, occurs when a shape can be divided into two identical halves by a line. If you fold the shape along this line, the two halves will perfectly overlap. The line of symmetry acts as a mirror, reflecting one half onto the other.
2. Rotational Symmetry
Rotational symmetry exists when a shape can be rotated about a central point by a certain angle (less than 360 degrees) and still look exactly the same. The angle of rotation is a fraction of 360 degrees, and the number of times the shape looks identical during a 360-degree rotation determines the order of rotational symmetry.
Exploring Different Quadrilaterals and Their Symmetry
To fully grasp the symmetry of a rectangle, it's beneficial to compare it to other quadrilaterals. A quadrilateral is a polygon with four sides. Let's examine some common quadrilaterals:
1. Square
A square is a special type of rectangle where all four sides are equal in length, and all four angles are right angles (90 degrees). A square exhibits a high degree of symmetry:
- Lines of Symmetry: A square possesses four lines of symmetry: two lines connecting opposite corners (diagonals) and two lines connecting the midpoints of opposite sides.
- Rotational Symmetry: A square also exhibits rotational symmetry of order 4. This means it can be rotated by 90, 180, and 270 degrees and still appear identical.
2. Rectangle
A rectangle is a quadrilateral with four right angles. Unlike a square, its opposite sides are equal in length, but not necessarily all sides are equal. We will explore its lines of symmetry in detail in the following sections.
3. Rhombus
A rhombus is a quadrilateral with all four sides equal in length. Its angles are not necessarily right angles. It has two lines of symmetry, both bisecting opposite angles.
4. Parallelogram
A parallelogram is a quadrilateral with opposite sides parallel and equal in length. A parallelogram, excluding squares and rectangles, generally has no lines of symmetry.
Determining the Lines of Symmetry in a Rectangle
Now, let's focus our attention on the rectangle. How many lines of symmetry does a rectangle possess? Unlike a square, a rectangle doesn't have diagonal lines of symmetry. To understand why, consider folding a non-square rectangle along a diagonal. The two halves will not overlap perfectly; the triangles formed will have different dimensions.
However, a rectangle does have lines of symmetry that run through the midpoints of opposite sides. These lines are perpendicular to the sides they bisect. Let's visualize this:
Imagine a rectangle ABCD, where A and B are adjacent vertices on one side, and C and D are adjacent vertices on the opposite side. The lines of symmetry are:
- A line connecting the midpoints of sides AB and CD: Folding the rectangle along this line will result in perfect overlap of the two halves.
- A line connecting the midpoints of sides BC and DA: Similarly, folding along this line will also result in perfect overlap.
Therefore, a rectangle has two lines of symmetry. These lines are always perpendicular to each other and bisect the rectangle into two congruent (identical) halves. They are crucial for understanding the rectangle's inherent balance and geometrical properties.
Real-World Applications of Rectangular Symmetry
Rectangular symmetry is prevalent in numerous aspects of our daily lives and various fields:
- Architecture: Many buildings, rooms, and windows exhibit rectangular symmetry, creating a sense of order and balance. This symmetry is aesthetically pleasing and contributes to structural integrity.
- Design: Graphic design, web design, and product design often utilize rectangular symmetry to create visually appealing and balanced compositions. Logos, posters, and websites frequently incorporate rectangular shapes and their symmetrical properties.
- Art: From paintings to sculptures, artists frequently use rectangular shapes and their inherent symmetry to create harmonious and balanced compositions. The principles of symmetry guide artistic choices and create a sense of stability and order.
- Engineering: Engineering designs, particularly in structural engineering, often utilize rectangular symmetry for stability and efficient material use. Rectangular structures are common because they provide stability and can distribute loads effectively.
- Nature: Although less common than rotational symmetry, some natural forms exhibit aspects of rectangular symmetry. Certain crystals or geological formations may have rectangular patterns.
Beyond Lines of Symmetry: Exploring Other Geometric Properties of Rectangles
While the number of lines of symmetry is a key aspect of a rectangle's geometry, it's important to acknowledge other defining properties:
- Four right angles: This is a defining characteristic, distinguishing rectangles from other quadrilaterals.
- Opposite sides are parallel and equal: This ensures the rectangle's stability and predictable geometric properties.
- Diagonals bisect each other: While not lines of symmetry, the diagonals of a rectangle intersect at their midpoints, creating four congruent triangles.
- Perimeter and area: Calculating the perimeter and area of a rectangle are fundamental geometric tasks, easily determined using the length and width.
Understanding these properties in conjunction with the lines of symmetry provides a complete picture of a rectangle's geometric characteristics.
Symmetry in Higher Dimensions: Extending the Concept
The concept of symmetry extends beyond two-dimensional shapes like rectangles. In three dimensions, objects can have planes of symmetry (analogous to lines of symmetry in 2D) and rotational symmetry about axes. A cube, for example, has multiple planes of symmetry and rotational symmetry. The principles of symmetry remain central to understanding geometric shapes in any dimension.
Conclusion: The Two Lines of Symmetry in a Rectangle – A Cornerstone of Geometry
In conclusion, a rectangle possesses two lines of symmetry, each connecting the midpoints of opposite sides. This relatively simple observation has significant implications in various fields, demonstrating the importance of symmetry in mathematics, design, and the world around us. Understanding the symmetry of rectangles provides a foundation for comprehending the properties of other geometric shapes and their applications in diverse areas. The seemingly simple question of "How many lines of symmetry does a rectangle have?" opens a gateway to a deeper appreciation of geometry and its pervasive influence on our lives. From the architecture of buildings to the design of everyday objects, the principles of symmetry play a pivotal role in shaping the world around us.
Latest Posts
Latest Posts
-
C 5 F 32 9 Solve For F
Mar 30, 2025
-
What Is The Gcf Of 16
Mar 30, 2025
-
Simplify The Square Root Of 162
Mar 30, 2025
-
An Excess Of Oxygen Reacts With 451 4 G Of Lead
Mar 30, 2025
-
Where Is The Majority Of The Earths Fresh Water Stored
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry In A Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
