Simplify The Square Root Of 162
listenit
Mar 30, 2025 · 4 min read
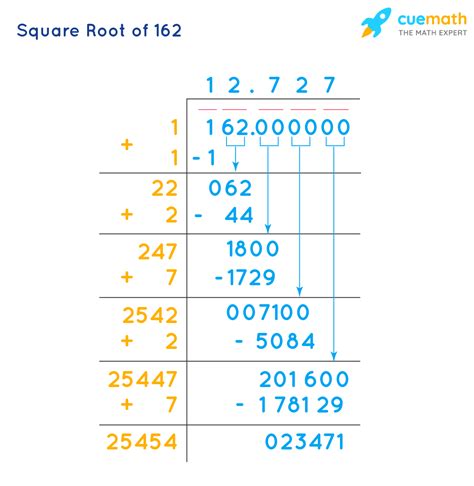
Table of Contents
Simplifying the Square Root of 162: A Comprehensive Guide
Simplifying square roots is a fundamental concept in mathematics, crucial for algebra, geometry, and beyond. While calculators can provide the decimal approximation, understanding the process of simplification allows for more precise mathematical manipulations and a deeper understanding of numbers. This article will delve into the simplification of the square root of 162, providing a step-by-step guide, exploring different approaches, and offering practice problems to solidify your understanding.
Understanding Square Roots and Simplification
Before diving into the simplification of √162, let's review the basics. A square root of a number x is a number that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. However, not all numbers have perfect square roots (i.e., whole number roots). This is where simplification comes in. Simplifying a square root involves expressing it in its simplest radical form, which means removing any perfect square factors from the radicand (the number inside the square root symbol).
Prime Factorization: The Key to Simplification
The most effective method for simplifying square roots is through prime factorization. Prime factorization involves breaking down a number into its prime factors—numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's apply this to 162:
- Find a pair of factors: We can start by noticing that 162 is an even number, so it's divisible by 2. 162 = 2 * 81.
- Continue factoring: 81 is a perfect square (9 * 9), but let's continue the prime factorization. 81 = 9 * 9 = 3 * 3 * 3 * 3.
- Prime factorization of 162: Therefore, the prime factorization of 162 is 2 * 3 * 3 * 3 * 3, or 2 * 3<sup>4</sup>.
Simplifying √162 using Prime Factorization
Now that we have the prime factorization of 162, we can simplify the square root:
√162 = √(2 * 3<sup>4</sup>)
Remember that √(a * b) = √a * √b. This property allows us to separate the factors:
√162 = √2 * √(3<sup>4</sup>)
Since √(3<sup>4</sup>) is the same as √(3² * 3²) = √(9 * 9) = 9, we can simplify further:
√162 = √2 * 9 or 9√2
Therefore, the simplified form of √162 is 9√2.
Alternative Approach: Identifying Perfect Square Factors
While prime factorization is the most robust method, you can also simplify by identifying perfect square factors directly.
Observe that 162 is divisible by 9 (a perfect square): 162 = 9 * 18.
Then, we can rewrite the square root as:
√162 = √(9 * 18) = √9 * √18 = 3√18
However, we notice that 18 also contains a perfect square factor (9): 18 = 9 * 2.
So, we can simplify further:
3√18 = 3√(9 * 2) = 3 * √9 * √2 = 3 * 3 * √2 = 9√2
This method arrives at the same simplified form: 9√2.
Why Simplification is Important
Simplifying square roots isn't just an exercise; it's essential for several reasons:
- Accuracy: Simplified forms are more precise than decimal approximations. Decimal approximations are often rounded, leading to slight inaccuracies in calculations, especially in complex problems.
- Efficiency: Simplified forms make calculations easier and faster. Working with 9√2 is more efficient than working with the decimal approximation of 12.7279...
- Clarity: Simplified forms enhance the clarity and readability of mathematical expressions. They provide a concise and elegant representation of the numerical value.
- Algebraic Manipulation: In algebra, working with simplified radicals is crucial for solving equations and simplifying expressions. It avoids unnecessary complications and improves the overall flow of the solution.
Practice Problems
To reinforce your understanding, let's try simplifying a few more square roots using the techniques we've learned:
- Simplify √72
- Simplify √200
- Simplify √486
- Simplify √1000
Solutions:
- √72 = √(36 * 2) = 6√2
- √200 = √(100 * 2) = 10√2
- √486 = √(81 * 6) = 9√6
- √1000 = √(100 * 10) = 10√10
Advanced Concepts: Working with Variables
The principles of simplifying square roots extend to expressions containing variables. Consider the expression √(162x⁴y⁶). We can simplify this by applying the same prime factorization technique to the numerical component (162) and using exponent rules for the variables:
√(162x⁴y⁶) = √(2 * 3⁴ * x⁴ * y⁶) = √(2) * √(3⁴) * √(x⁴) * √(y⁶) = 9x²y³√2
This demonstrates how the simplification methods seamlessly integrate with algebraic expressions.
Conclusion: Mastering Square Root Simplification
Mastering the simplification of square roots, as demonstrated through the example of √162, is a fundamental skill in mathematics. By consistently applying prime factorization or identifying perfect square factors, you can express square roots in their simplest, most efficient, and accurate forms. This skill is not merely a computational exercise; it's a cornerstone for success in higher-level mathematics and problem-solving across various disciplines. Remember to practice regularly to build fluency and confidence in tackling more complex radical expressions. The more you practice, the easier and more intuitive the process will become.
Latest Posts
Latest Posts
-
Solve This Equation 4y 228 352
Apr 01, 2025
-
Oxidation Reactions Are Coupled With Reactions
Apr 01, 2025
-
Whats Half Of 1 And 1 2
Apr 01, 2025
-
Why Is Water Liquid At Room Temperature
Apr 01, 2025
-
How To Determine The Density Of A Solid
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 162 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
