How Many 1/6 Are In 2/3
listenit
May 25, 2025 · 5 min read
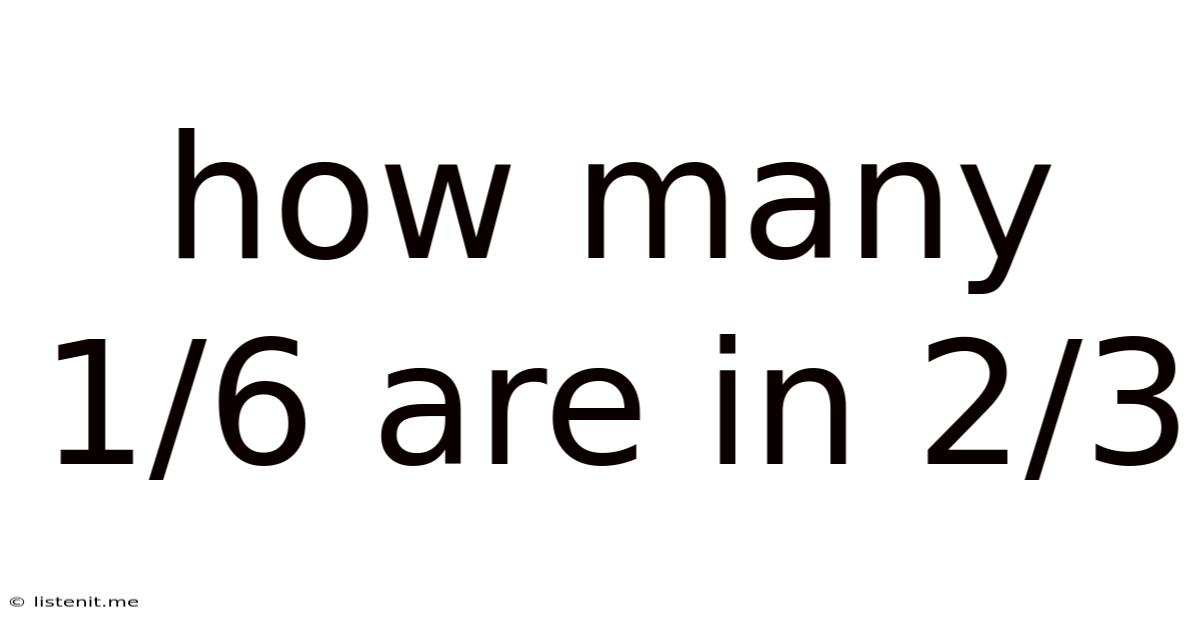
Table of Contents
How Many 1/6s are in 2/3? A Comprehensive Guide to Fraction Division
Understanding fractions is a fundamental concept in mathematics, essential for various applications in everyday life and advanced studies. This article delves into the question, "How many 1/6 are in 2/3?", providing a comprehensive explanation using various methods to solidify your understanding of fraction division. We'll go beyond a simple answer, exploring the underlying principles and offering practical examples to enhance your problem-solving skills.
Understanding the Question: Dividing Fractions
The core of the problem lies in understanding what it means to ask "how many 1/6 are in 2/3?". This is fundamentally a division problem. We're looking to determine how many times the fraction 1/6 fits into the fraction 2/3. This can be expressed mathematically as:
(2/3) ÷ (1/6) = ?
Several methods can solve this division problem, each illustrating different aspects of fraction manipulation. We'll explore these methods in detail below.
Method 1: Reciprocal and Multiplication
This is perhaps the most common and efficient method for dividing fractions. The rule states that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down.
-
Find the reciprocal of 1/6: The reciprocal of 1/6 is 6/1, or simply 6.
-
Rewrite the division as multiplication: Our problem now becomes:
(2/3) x (6/1) = ?
-
Multiply the numerators and the denominators:
(2 x 6) / (3 x 1) = 12/3
-
Simplify the result:
12/3 simplifies to 4
Therefore, there are four 1/6s in 2/3.
Visual Representation of Method 1
Imagine a pizza cut into 6 equal slices. 2/3 of the pizza represents 4 slices (2/3 * 6 = 4). Each slice is 1/6 of the pizza. Since there are 4 slices, there are 4 (1/6)s in 2/3. This visual representation helps solidify the mathematical result.
Method 2: Finding a Common Denominator
This method emphasizes the importance of common denominators in comparing and manipulating fractions.
-
Find a common denominator for 2/3 and 1/6: The least common multiple of 3 and 6 is 6.
-
Rewrite the fractions with the common denominator:
- 2/3 can be rewritten as 4/6 (multiply both numerator and denominator by 2).
-
Now compare the fractions: How many 1/6s are in 4/6?
-
The answer is clearly 4.
Advantages and Disadvantages of Method 2
This method offers a more intuitive approach for those comfortable working with equivalent fractions. It visually demonstrates the relationship between the two fractions. However, it can be less efficient than the reciprocal method for more complex fraction division problems.
Method 3: Using Decimal Equivalents
This method uses decimal representation to solve the problem. While perhaps less elegant than the previous methods, it reinforces the connection between fractions and decimals.
-
Convert the fractions to decimals:
- 2/3 ≈ 0.6667 (repeating decimal)
- 1/6 ≈ 0.1667 (repeating decimal)
-
Divide the decimal equivalents:
- 0.6667 ÷ 0.1667 ≈ 4
Again, we arrive at the answer of 4.
Limitations of Method 3
The use of decimal approximations introduces a small margin of error, especially with repeating decimals. This method is less precise than working directly with fractions, and it's generally recommended to stick to fraction manipulation for accuracy.
Real-World Applications of Fraction Division
Understanding fraction division is crucial in many real-world scenarios. Consider these examples:
-
Baking: A recipe calls for 2/3 cup of flour, and each scoop holds 1/6 cup. How many scoops are needed? (Answer: 4)
-
Construction: A project requires 2/3 of a roll of wire, and each section uses 1/6 of a roll. How many sections can be made? (Answer: 4)
-
Sewing: A project needs 2/3 of a yard of fabric, and each piece requires 1/6 of a yard. How many pieces can be cut? (Answer: 4)
These are just a few examples; the application of fraction division extends to numerous fields, including finance, engineering, and cooking.
Expanding Your Understanding of Fraction Operations
Mastering fraction division builds a solid foundation for more complex mathematical concepts. Here are some related topics to explore further:
-
Mixed numbers: Learn to divide fractions involving mixed numbers (e.g., 1 1/2 ÷ 1/4).
-
Complex fractions: Practice solving problems with fractions in both the numerator and denominator.
-
Fraction multiplication and addition/subtraction: Reinforce your understanding of these fundamental fraction operations.
By practicing these various techniques, you will not only improve your understanding of fractions but also enhance your overall mathematical proficiency.
Conclusion: Mastering Fractions for Success
This comprehensive guide explored different methods for solving the problem, "How many 1/6s are in 2/3?". We've demonstrated that the answer is 4 using the reciprocal method, the common denominator method, and the decimal equivalent method. Understanding these different approaches helps to solidify your understanding of fraction division and allows you to choose the most efficient method depending on the specific problem. Remember that mastering fractions is a key building block for success in various mathematical and real-world applications. By practicing consistently and exploring related concepts, you will enhance your mathematical skills and confidently tackle more challenging problems. The ability to manipulate and understand fractions is a valuable asset in many aspects of life, both personal and professional. Continue practicing, and soon you'll be a fraction expert!
Latest Posts
Latest Posts
-
Greatest Common Factor Of 20 And 25
May 25, 2025
-
What Is 45 99 In Simplest Form
May 25, 2025
-
80 Is 25 Percent Of What Number
May 25, 2025
-
What Is 3 4 Minus 1 3
May 25, 2025
-
What Is A Prime Factorization Of 90
May 25, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/6 Are In 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.