80 Is 25 Percent Of What Number
listenit
May 25, 2025 · 5 min read
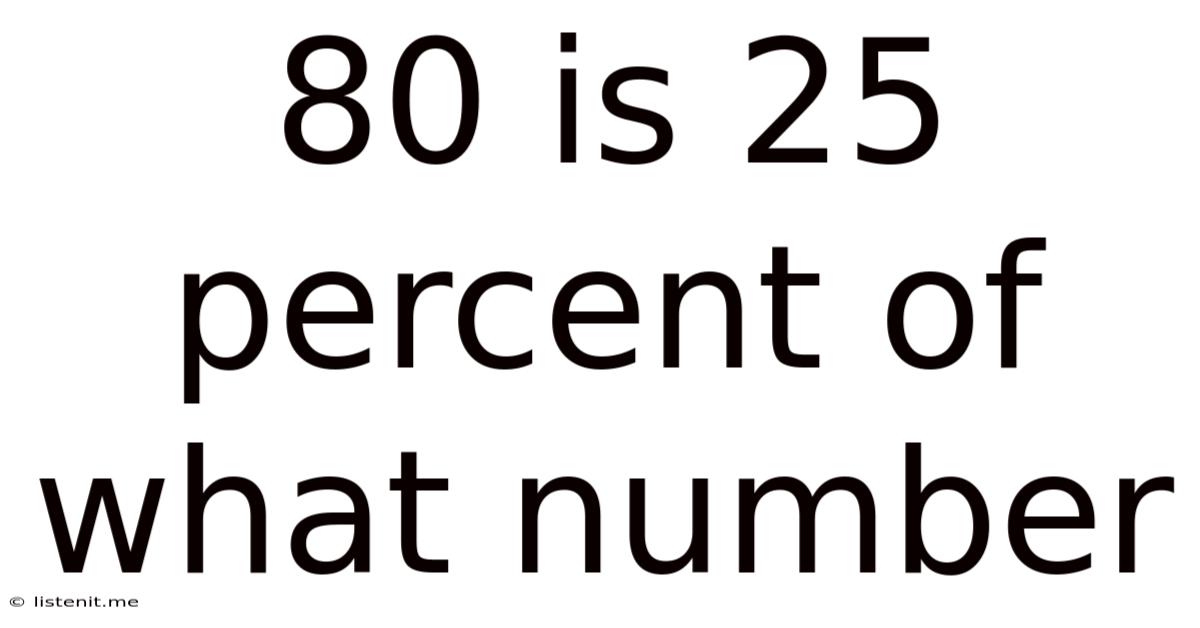
Table of Contents
80 is 25 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the question, "80 is 25 percent of what number?", providing not only the solution but also a comprehensive exploration of the underlying concepts and methods for solving percentage problems. We will explore different approaches, including algebraic methods, using proportions, and utilizing the concept of percentage as a fraction. This detailed guide will empower you to confidently tackle similar percentage problems in the future.
Understanding the Problem: Deconstructing "80 is 25% of What Number?"
The statement "80 is 25 percent of what number?" presents a classic percentage problem. We are given a part (80) and a percentage (25%), and we need to find the whole number. This is a common scenario encountered in various contexts, making it crucial to master the solution techniques.
Let's break down the components:
- 80: This represents the part or portion of the whole number we're trying to find.
- 25%: This is the percentage representing the relationship between the part (80) and the whole.
- What number?: This is the unknown value, the whole number we are trying to calculate.
Method 1: Using Algebra to Solve for the Unknown
Algebra provides a powerful and straightforward method to solve percentage problems. We can represent the unknown number with a variable, such as 'x'. Then, we translate the problem into an algebraic equation:
80 = 0.25 * x
This equation states that 80 is equal to 25% (expressed as a decimal, 0.25) of x. To solve for x, we isolate it by dividing both sides of the equation by 0.25:
x = 80 / 0.25
x = 320
Therefore, 80 is 25% of 320.
Method 2: Solving with Proportions
Proportions offer another elegant approach to solving percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion to represent the relationship between the part, the whole, and the percentage:
Part / Whole = Percentage / 100
In our problem:
80 / x = 25 / 100
To solve this proportion, we cross-multiply:
80 * 100 = 25 * x
8000 = 25x
Now, we divide both sides by 25 to isolate x:
x = 8000 / 25
x = 320
Again, we find that 80 is 25% of 320.
Method 3: Utilizing the Percentage as a Fraction
Percentages can be easily expressed as fractions. 25% is equivalent to the fraction 25/100, which simplifies to 1/4. We can rewrite the problem as:
80 = (1/4) * x
To solve for x, we multiply both sides by 4:
x = 80 * 4
x = 320
This method confirms our previous results: 80 is 25% of 320.
Real-World Applications: Where Percentage Calculations Matter
Understanding how to calculate percentages is essential in numerous everyday situations. Here are just a few examples:
-
Shopping and Discounts: Calculating the final price of an item after a discount is applied. For instance, if a $100 item is 20% off, you'd calculate 20% of $100 and subtract it from the original price.
-
Taxes and Fees: Determining the total cost of a purchase including sales tax or service fees. This involves calculating the tax amount based on a percentage of the price and adding it to the original cost.
-
Financial Planning: Calculating interest earned on savings accounts, investment returns, or loan payments. These calculations rely heavily on understanding percentages and compound interest.
-
Data Analysis: Interpreting data presented in percentage form, such as market share statistics, survey results, or demographic information. This requires the ability to comprehend and compare different percentages.
-
Cooking and Baking: Scaling recipes up or down. If a recipe calls for 25% water of the total ingredient weight, you need to calculate the amount based on the total weight.
Advanced Percentage Problems and Techniques
While the problem "80 is 25% of what number?" is a foundational percentage problem, more complex scenarios exist. These often involve multiple percentages, finding percentage increases or decreases, or working with compound percentages.
Let's look at a slightly more complex example:
"A product's price increased by 15% to $115. What was the original price?"
Here, we don't directly have the original percentage. Instead, we know the final price after a percentage increase. To solve this, we can set up an equation:
Original Price * 1.15 = $115
Solving for the original price:
Original Price = $115 / 1.15
Original Price = $100
This demonstrates how manipulating the equation to fit the given information is key to solving complex percentage problems.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can greatly simplify calculations.
-
Practice regularly: The more percentage problems you solve, the more comfortable and efficient you'll become.
-
Use a calculator when needed: Don't hesitate to use a calculator for more complex calculations, ensuring accuracy and speed.
-
Check your work: Always double-check your answers to ensure they are logical and consistent with the problem's context.
Conclusion: Building a Strong Foundation in Percentages
The ability to solve percentage problems like "80 is 25 percent of what number?" is a valuable skill that extends far beyond the classroom. From managing personal finances to analyzing data in professional settings, mastering percentage calculations empowers you to confidently navigate numerous real-world scenarios. By understanding the different methods – algebraic solutions, proportions, and fractional representations – and practicing regularly, you can build a strong foundation in percentages and apply this knowledge to solve a wide array of problems with ease and accuracy. Remember to break down the problem into its constituent parts, choose the method that best suits your understanding, and always double-check your work. With consistent practice, you will become proficient in solving even the most complex percentage calculations.
Latest Posts
Latest Posts
-
1 6 X 1 3 As A Fraction
May 25, 2025
-
Express The Following Numbers In Scientific Notation
May 25, 2025
-
2 7 1 4 As A Fraction
May 25, 2025
-
What Is 18 Minutes From Now
May 25, 2025
-
Write 8 4 5 As A Decimal Number
May 25, 2025
Related Post
Thank you for visiting our website which covers about 80 Is 25 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.