1/6 X 1/3 As A Fraction
listenit
May 25, 2025 · 5 min read
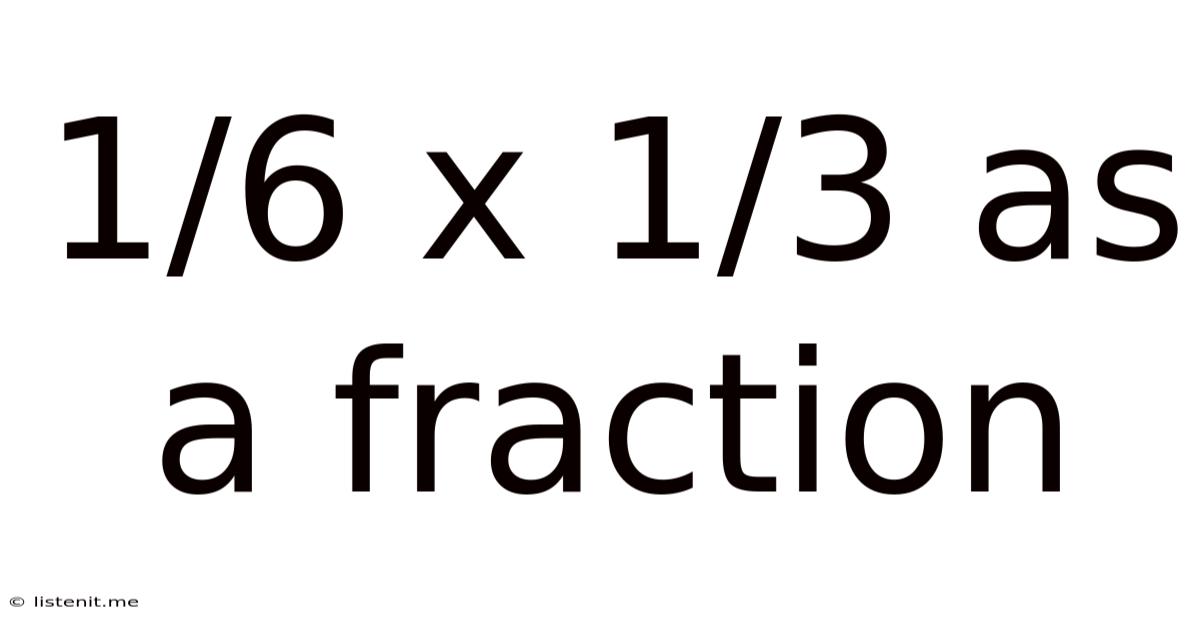
Table of Contents
1/6 x 1/3 as a Fraction: A Comprehensive Guide
Understanding fraction multiplication is a fundamental skill in mathematics. This comprehensive guide will delve into the process of multiplying fractions, specifically addressing the problem of 1/6 x 1/3, providing a step-by-step explanation, exploring related concepts, and offering practical applications. We'll also examine how this concept relates to other mathematical operations and why understanding it is crucial for further mathematical exploration.
Understanding Fractions
Before we tackle the multiplication of 1/6 and 1/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Multiplying Fractions: The Basic Rule
The process of multiplying fractions is remarkably straightforward. The rule is simple: multiply the numerators together and multiply the denominators together. This can be expressed as:
(a/b) x (c/d) = (a x c) / (b x d)
Where 'a', 'b', 'c', and 'd' represent integers, and 'b' and 'd' are not zero (division by zero is undefined).
Solving 1/6 x 1/3
Now, let's apply this rule to solve 1/6 x 1/3:
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 6 x 3 = 18
Therefore, the result of 1/6 x 1/3 is 1/18.
This means that one-sixth of one-third is equal to one-eighteenth. Visually, imagine dividing a rectangle into six equal parts horizontally and then dividing each of those six parts into three equal parts vertically. You would end up with 18 smaller, equal rectangles. One of those 18 smaller rectangles represents 1/18 of the original whole.
Simplifying Fractions
While 1/18 is the correct answer, it's crucial to understand the concept of simplifying fractions. Simplifying a fraction means reducing it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
In the case of 1/18, the GCD of 1 and 18 is 1. Since dividing both the numerator and denominator by 1 doesn't change the value of the fraction, 1/18 is already in its simplest form.
Visualizing Fraction Multiplication
Visual aids can be incredibly helpful in understanding fraction multiplication. Consider using diagrams, such as area models or fraction circles, to represent the fractions and their multiplication. This concrete representation can solidify the abstract concept and improve comprehension. For example, a visual representation of 1/6 x 1/3 would show a shaded area representing one-eighteenth of a whole.
Relating to Other Mathematical Operations
Fraction multiplication is closely related to other mathematical operations:
- Division: Dividing by a fraction is the same as multiplying by its reciprocal. For example, 1/6 ÷ 3 is the same as 1/6 x (1/3) = 1/18.
- Addition and Subtraction: Before adding or subtracting fractions, you need to find a common denominator. This isn't directly part of multiplication, but understanding common denominators is crucial for working with fractions in general.
Practical Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous real-world applications:
- Cooking and Baking: Scaling recipes up or down frequently involves multiplying fractions. If a recipe calls for 1/2 cup of flour, and you want to make half the recipe, you'll need to multiply 1/2 by 1/2.
- Construction and Measurement: Precise measurements in construction and carpentry often involve fractions. Multiplying fractions is necessary when calculating areas or volumes.
- Finance: Calculating interest, discounts, or portions of investments often involves working with fractions and their multiplication.
- Data Analysis: When dealing with percentages or proportions in data analysis, you often encounter and utilize fraction multiplication.
Advanced Concepts and Extensions
Beyond the basic multiplication of simple fractions like 1/6 x 1/3, understanding fraction multiplication extends to more complex scenarios:
- Multiplying mixed numbers: A mixed number combines a whole number and a fraction (e.g., 1 1/2). To multiply mixed numbers, you first convert them into improper fractions (where the numerator is greater than the denominator) before applying the standard multiplication rule.
- Multiplying fractions with variables: Algebra introduces the concept of multiplying fractions containing variables. The process remains the same – multiply numerators and denominators – but the result will contain variables.
Troubleshooting Common Mistakes
When working with fractions, some common mistakes can occur:
- Incorrectly multiplying numerators and denominators: Always remember to multiply numerators together and denominators together separately.
- Forgetting to simplify: Always simplify the resulting fraction to its lowest terms.
- Errors in converting mixed numbers: Ensure you correctly convert mixed numbers into improper fractions before multiplication.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is essential for success in mathematics and its numerous applications in everyday life. By understanding the basic rule, practicing with examples (like 1/6 x 1/3), and visualizing the process, you can confidently tackle more complex fraction problems and apply this skill to various real-world scenarios. Remember to always simplify your answers and be mindful of common mistakes. Consistent practice and a solid understanding of the underlying concepts will pave the way for success in more advanced mathematical topics. The seemingly simple problem of 1/6 x 1/3 serves as a gateway to a deeper understanding of the world of fractions and their significant role in mathematics and beyond. Through thorough understanding and consistent practice, you can build a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 10 Of 50000 Dollars
May 25, 2025
-
Greatest Common Factor Of 34 And 85
May 25, 2025
-
How Old Am I Born In 1974
May 25, 2025
-
6 Is What Percent Of 21
May 25, 2025
-
119 Divided By 4 With Remainder
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1/6 X 1/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.