What Is 3 4 Minus 1 3
listenit
May 25, 2025 · 6 min read
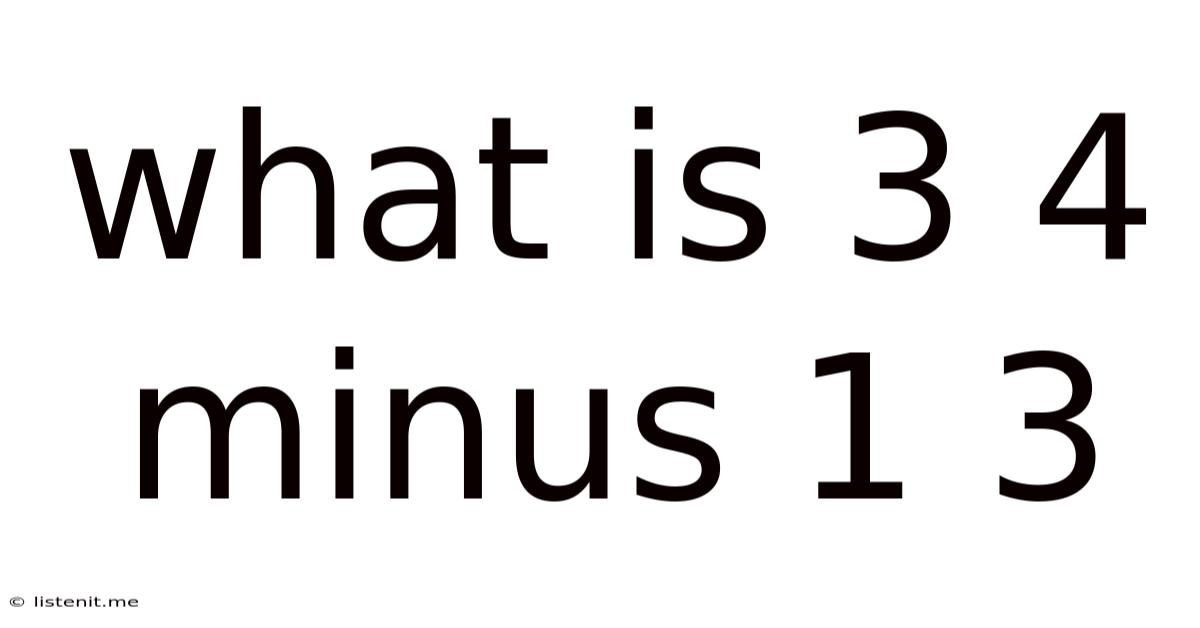
Table of Contents
What is 3/4 Minus 1/3? A Deep Dive into Fraction Subtraction
This seemingly simple question, "What is 3/4 minus 1/3?", opens a door to a fundamental area of mathematics: fraction subtraction. While the calculation itself is straightforward, understanding the underlying principles provides a solid foundation for more complex mathematical operations. This article delves into the process of subtracting fractions, exploring various methods, offering practical examples, and explaining the significance of this concept in everyday life and advanced mathematical applications.
Understanding Fractions: A Refresher
Before tackling the subtraction, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts. Therefore, 3/4 represents three-quarters of a whole.
The Challenge of Subtracting Unlike Fractions
Subtracting fractions directly is only possible when they share the same denominator (they are "like" fractions). Our problem presents us with "unlike" fractions: 3/4 and 1/3. To subtract them, we must first find a common denominator.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find the smallest common multiple. For 4 and 3:
- Multiples of 4: 4, 8, 12, 16, 20...
- Multiples of 3: 3, 6, 9, 12, 15...
- The smallest common multiple is 12.
-
Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in either denominator.
- 4 = 2 x 2 = 2²
- 3 = 3
- LCD = 2² x 3 = 12
Once we've established the LCD (12), we can proceed with the subtraction.
Converting to Equivalent Fractions
Now that we have the LCD (12), we need to convert both fractions into equivalent fractions with this denominator. This is done by multiplying both the numerator and the denominator of each fraction by the appropriate factor:
-
For 3/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3 (because 4 x 3 = 12): (3 x 3) / (4 x 3) = 9/12
-
For 1/3: To get a denominator of 12, we multiply both the numerator and the denominator by 4 (because 3 x 4 = 12): (1 x 4) / (3 x 4) = 4/12
Performing the Subtraction
With both fractions now having the same denominator (12), we can subtract the numerators directly:
9/12 - 4/12 = (9 - 4) / 12 = 5/12
Therefore, 3/4 minus 1/3 equals 5/12.
Visualizing Fraction Subtraction
Visual aids can greatly enhance understanding, especially for those new to fraction manipulation. Imagine two pizzas, each cut into a different number of slices:
- Pizza 1 (representing 3/4): Cut into 4 slices, with 3 slices representing the portion we have.
- Pizza 2 (representing 1/3): Cut into 3 slices, with 1 slice representing the portion we have.
To compare and subtract, we need to find a common way to represent both portions using the same size slices. If we cut Pizza 1 into 12 equal slices (3 times more slices) and Pizza 2 into 12 equal slices (4 times more slices), we can easily visualize the subtraction.
Pizza 1 would have 9 out of 12 slices (9/12), and Pizza 2 would have 4 out of 12 slices (4/12). Subtracting the slices, we're left with 5 out of 12 slices (5/12). This visual representation reinforces the result obtained through the mathematical calculation.
Real-World Applications of Fraction Subtraction
Fraction subtraction is not confined to the classroom; it finds practical applications in various aspects of daily life:
-
Cooking and Baking: Adjusting recipes, calculating ingredient quantities, and determining the remaining portions. If a recipe calls for 3/4 cup of flour, and you've already used 1/3 cup, you can easily calculate the remaining flour using subtraction.
-
Measuring and Construction: Precise measurements in construction, carpentry, and other trades heavily rely on fraction subtraction for accurate calculations. Imagine subtracting the length of a piece of wood that's been cut from a larger piece.
-
Finance and Budgeting: Tracking expenses, managing budgets, and calculating remaining funds. If your budget allocates 3/4 of your monthly income to expenses, and you’ve spent 1/3, calculating the remaining portion is crucial for financial planning.
-
Time Management: Calculating the remaining time for tasks. For instance, if a project requires 3/4 of a day and you've already spent 1/3 of a day, subtraction can help you determine the remaining time.
Expanding on Fraction Subtraction: Mixed Numbers
The concepts discussed so far apply equally to subtracting mixed numbers (numbers composed of a whole number and a fraction). Let's consider an example: 2 3/4 - 1 1/3.
-
Convert Mixed Numbers to Improper Fractions: This involves converting the mixed numbers into fractions where the numerator is greater than the denominator.
- 2 3/4 = (2 x 4 + 3) / 4 = 11/4
- 1 1/3 = (1 x 3 + 1) / 3 = 4/3
-
Find the LCD: The LCD of 4 and 3 is 12.
-
Convert to Equivalent Fractions:
- 11/4 = (11 x 3) / (4 x 3) = 33/12
- 4/3 = (4 x 4) / (3 x 4) = 16/12
-
Subtract:
- 33/12 - 16/12 = 17/12
-
Convert back to Mixed Number (if needed): 17/12 can be converted back to a mixed number: 1 5/12
Therefore, 2 3/4 - 1 1/3 = 1 5/12.
Advanced Applications in Mathematics
Fraction subtraction forms the basis for numerous advanced mathematical concepts and applications:
-
Algebra: Solving equations involving fractions requires a solid understanding of fraction subtraction.
-
Calculus: Derivatives and integrals often involve manipulations of fractions and require proficiency in fraction arithmetic.
-
Linear Algebra: Matrix operations and vector calculations frequently necessitate operations with fractions.
-
Probability and Statistics: Calculating probabilities and analyzing statistical data often involve fractional calculations.
Conclusion: Mastering Fraction Subtraction for a Brighter Future
While seemingly simple, the subtraction of fractions, such as 3/4 minus 1/3, underpins a vast array of mathematical concepts and real-world applications. Understanding the process, from finding the least common denominator to converting fractions and performing the subtraction, provides a fundamental building block for more advanced mathematical pursuits. Mastering these skills empowers individuals to tackle complex problems with confidence, paving the way for success in various academic and professional endeavors. By grasping the core principles and applying them consistently, one can unlock a deeper appreciation for the beauty and practicality of mathematics.
Latest Posts
Latest Posts
-
10 Is What Percent Of 27
May 25, 2025
-
5 8 Plus 5 8 Equals
May 25, 2025
-
How Many Btus Do You Need Per Square Foot
May 25, 2025
-
What Is 1 10 Of 3 000
May 25, 2025
-
What Is 4 Weeks From Now
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Minus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.