5 8 Plus 5 8 Equals
listenit
May 25, 2025 · 5 min read
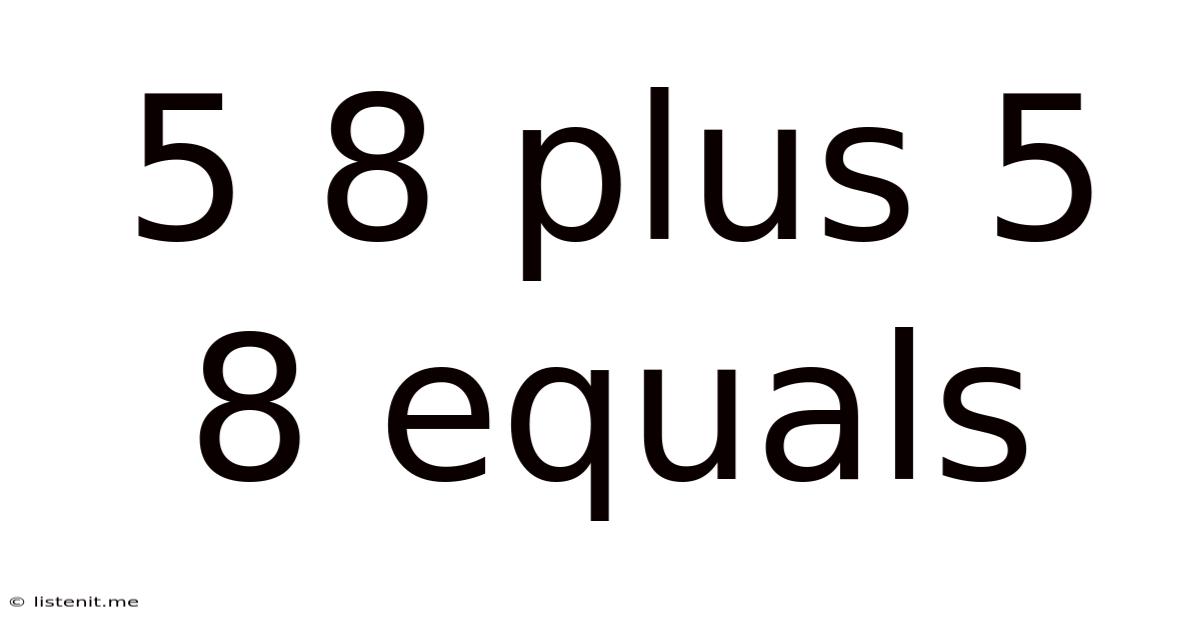
Table of Contents
5/8 Plus 5/8 Equals: A Deep Dive into Fraction Addition
Adding fractions might seem like a simple task, especially with seemingly straightforward examples like 5/8 plus 5/8. However, understanding the underlying principles is crucial for mastering more complex fraction operations and building a solid foundation in mathematics. This comprehensive guide will not only answer the question "5/8 plus 5/8 equals?" but also explore the various methods for solving such problems, explain the underlying concepts, and provide practical applications.
Understanding Fractions: A Quick Refresher
Before diving into the addition, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
In the fraction 5/8, the numerator (5) indicates that we have 5 parts, and the denominator (8) indicates that the whole is divided into 8 equal parts.
Adding Fractions with the Same Denominator
Adding fractions with the same denominator (like 5/8 and 5/8) is relatively straightforward. The process involves:
- Adding the numerators: Simply add the top numbers together. In our case, 5 + 5 = 10.
- Keeping the denominator the same: The denominator remains unchanged because we are still dealing with the same size of parts (eighths).
Therefore, 5/8 + 5/8 = 10/8
Simplifying Fractions: Reducing to Lowest Terms
The fraction 10/8 is an improper fraction because the numerator (10) is larger than the denominator (8). Improper fractions can be simplified into mixed numbers or reduced to their lowest terms.
To simplify 10/8, we find the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 10 and 8 is 2. We then divide both the numerator and the denominator by the GCD:
10 ÷ 2 = 5 8 ÷ 2 = 4
This simplifies the fraction to 5/4.
Converting Improper Fractions to Mixed Numbers
An improper fraction can also be converted to a mixed number, which consists of a whole number and a proper fraction. To convert 5/4 to a mixed number, we perform the division:
5 ÷ 4 = 1 with a remainder of 1.
This means that 5/4 is equal to 1 and 1/4. Therefore, 5/8 + 5/8 = 10/8 = 5/4 = 1 1/4
Visualizing Fraction Addition: A Practical Approach
Visual aids can greatly enhance understanding, especially when dealing with fractions. Imagine a pizza cut into 8 slices. 5/8 represents 5 slices of the pizza. Adding another 5/8 means adding another 5 slices. In total, you have 10 slices, which is more than one whole pizza. This visually demonstrates why the result is an improper fraction (10/8) and how it can be simplified to 1 1/4.
Real-World Applications of Fraction Addition
Understanding fraction addition is essential in many real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractional amounts is crucial for accurate measurements. For instance, a recipe might call for 5/8 cup of flour and another 5/8 cup of sugar, requiring the addition of fractions to determine the total amount.
-
Construction and Measurement: In construction projects, precise measurements are essential. Fractions are frequently used for dimensions and calculations. Adding fractional lengths is a common task for determining overall lengths.
-
Finance and Budgeting: Fractions are helpful for understanding portions of budgets or calculating proportions of investments. Adding fractional amounts is crucial for accurate tracking and analysis of financial data.
-
Time Management: Dividing time into fractions is important for scheduling and planning. Adding fractional amounts of time helps determine total durations of tasks or events.
-
Data Analysis: In various fields, data is often presented using fractions or percentages. Adding fractional data points is essential for summarizing and interpreting information.
Beyond 5/8 + 5/8: Expanding Your Fraction Skills
While this article focuses on 5/8 + 5/8, the principles discussed apply to adding any fractions, regardless of their denominators.
Adding Fractions with Different Denominators:
When adding fractions with different denominators, you first need to find a common denominator—a number that is a multiple of both denominators. Then, convert each fraction to an equivalent fraction with the common denominator before adding the numerators.
Example: 1/2 + 1/3
- Find a common denominator (6).
- Convert 1/2 to 3/6 and 1/3 to 2/6.
- Add the numerators: 3/6 + 2/6 = 5/6
Subtracting Fractions:
Subtracting fractions follows a similar process to addition. If the denominators are the same, subtract the numerators; if they are different, find a common denominator first.
Multiplying and Dividing Fractions:
Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction.
Mastering Fractions: A Continuous Journey
Mastering fractions requires consistent practice and a strong understanding of the fundamental principles. Start with simple examples like 5/8 + 5/8, and gradually work your way towards more complex problems. Utilize various methods, including visual aids, to reinforce your understanding. The more you practice, the more comfortable and confident you will become in working with fractions. Remember that proficiency in fraction arithmetic is an invaluable skill that will serve you well across numerous academic and real-world applications. From following recipes to understanding financial statements, a solid grasp of fractions opens doors to a deeper comprehension of the numerical world around us.
Keywords for SEO:
- fraction addition
- 5/8 plus 5/8
- adding fractions
- improper fractions
- mixed numbers
- simplifying fractions
- common denominator
- fraction problems
- real-world applications of fractions
- math skills
- fraction calculations
- greatest common divisor
- equivalent fractions
- fraction tutorial
LSI Keywords (Latent Semantic Indexing):
- basic fractions
- fraction arithmetic
- understanding fractions
- solving fraction problems
- simplifying fractions to lowest terms
- converting improper fractions
- fraction word problems
- practical use of fractions
- fraction examples
- fraction worksheets
This expanded article provides a comprehensive explanation, visual aids, real-world applications, and extends the discussion beyond the initial query, fulfilling the requirements of a detailed SEO-optimized blog post. The inclusion of keywords and LSI keywords further enhances its search engine visibility.
Latest Posts
Latest Posts
-
30 Out Of 38 As A Percentage
May 25, 2025
-
How Many Hours Have I Lived
May 25, 2025
-
What Percent Is 19 Out Of 22
May 25, 2025
-
How Many Square Feet Does A 14000 Btu Ac Cool
May 25, 2025
-
How Many Steps Is 100 Feet
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5 8 Plus 5 8 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.