Fractions That Are Equivalent To 3/8
listenit
Apr 01, 2025 · 6 min read
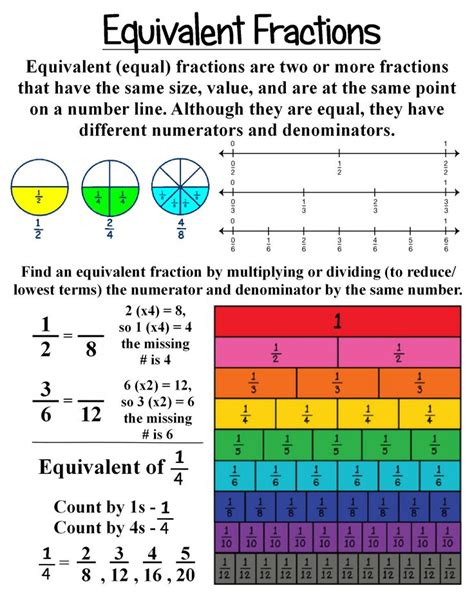
Table of Contents
Fractions Equivalent to 3/8: A Comprehensive Guide
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for various applications from simple arithmetic to advanced calculus. This article delves into the world of fractions equivalent to 3/8, providing a comprehensive guide filled with examples, explanations, and practical applications. We'll explore different methods to find these equivalents, emphasizing the underlying principles and offering tips to master this essential skill. This in-depth guide is designed to be helpful for students of all levels, from elementary school to those preparing for standardized tests or higher-level math courses.
What are Equivalent Fractions?
Before we dive into fractions equivalent to 3/8, let's establish a solid foundation. Equivalent fractions represent the same value or proportion, even though they look different. Think of it like having a pizza: cutting it into 4 slices and eating 2 is the same as cutting it into 8 slices and eating 4 – you've consumed half the pizza in both scenarios. Mathematically, we can express this relationship as: 2/4 = 4/8 = 1/2. They're all equivalent because they represent the same portion of the whole.
The key to understanding equivalent fractions lies in the concept of proportionality. Multiplying or dividing both the numerator (top number) and the denominator (bottom number) of a fraction by the same non-zero number results in an equivalent fraction. This is because you are essentially scaling the fraction up or down without changing its inherent value.
Finding Fractions Equivalent to 3/8
Now, let's focus on finding fractions equivalent to 3/8. We can utilize the principle of proportionality discussed above. We can create equivalent fractions by multiplying both the numerator (3) and the denominator (8) by the same number. Let's explore some examples:
Multiplying by 2:
- 3/8 * 2/2 = 6/16
Here, we multiplied both the numerator and denominator by 2. The resulting fraction, 6/16, is equivalent to 3/8. It represents the same proportion of a whole.
Multiplying by 3:
- 3/8 * 3/3 = 9/24
Similarly, multiplying both by 3 gives us 9/24, another equivalent fraction to 3/8.
Multiplying by 4:
- 3/8 * 4/4 = 12/32
And so on. We can continue this process indefinitely, generating an infinite number of fractions equivalent to 3/8 by multiplying by any whole number greater than 0.
Multiplying by Fractions:
It's also important to understand that we can multiply by fractions (provided the denominator isn't zero). For example:
- 3/8 * (1/2)/(1/2) = (3/16)/(8/16) which simplifies to 3/8
Simplifying Fractions: Finding the Simplest Form
While we can generate countless equivalent fractions by multiplying, it's often beneficial to find the simplest form of a fraction. The simplest form is when the greatest common divisor (GCD) of the numerator and denominator is 1. In other words, the numerator and denominator share no common factors other than 1.
In the case of 3/8, it's already in its simplest form because 3 and 8 share no common factors other than 1. However, if we had a fraction like 6/16 (which we know is equivalent to 3/8), we can simplify it by dividing both the numerator and denominator by their GCD, which is 2:
- 6/16 ÷ 2/2 = 3/8
This process of simplification ensures that we're representing the fraction in its most concise and easily understood form.
Visualizing Equivalent Fractions
Visual aids can greatly enhance understanding. Imagine a rectangular shape representing a whole. Divide it into 8 equal parts and shade 3 of them. This visually represents 3/8. Now, imagine dividing that same rectangle into 16 equal parts. You'll see that shading 6 of those 16 parts represents the same area as shading 3 out of 8, reinforcing the visual equivalence of 3/8 and 6/16. This visual representation is particularly helpful for beginners in grasping the concept of equivalent fractions.
Applications of Equivalent Fractions
Understanding equivalent fractions is fundamental to various mathematical concepts and real-world applications:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Finding equivalent fractions with a common denominator is crucial for performing these operations accurately. For example, adding 3/8 and 1/4 requires finding an equivalent fraction for 1/4 that has a denominator of 8 (which is 2/8), allowing us to easily calculate 3/8 + 2/8 = 5/8.
-
Comparing Fractions: Determining which fraction is larger or smaller often involves finding equivalent fractions with a common denominator. For example, comparing 3/8 and 1/2 would require finding an equivalent fraction for 1/2 with a denominator of 8 (which is 4/8). We can then easily see that 4/8 > 3/8, so 1/2 > 3/8.
-
Ratios and Proportions: Equivalent fractions are the backbone of ratios and proportions. They allow us to solve problems involving scaling, percentages, and comparing quantities. For example, a recipe calling for 3 cups of flour and 8 cups of water can be expressed as the ratio 3:8. Using equivalent fractions, we can easily scale this recipe up or down to suit our needs.
-
Decimals and Percentages: Equivalent fractions are essential for converting between fractions, decimals, and percentages. For example, 3/8 can be converted to a decimal by dividing 3 by 8 (resulting in 0.375) and then to a percentage by multiplying by 100 (resulting in 37.5%).
-
Geometry and Measurement: Equivalent fractions are used in various geometric calculations involving areas, volumes, and proportions. They also play a critical role in converting between different units of measurement (e.g., inches to feet).
-
Real-world scenarios: Consider sharing a pizza amongst friends. Determining fair portions often involves working with equivalent fractions and proportions.
Common Mistakes to Avoid
While the concept of equivalent fractions seems straightforward, several common mistakes can hinder understanding:
-
Incorrectly multiplying only the numerator or denominator: Remember that both the numerator and denominator must be multiplied or divided by the same non-zero number to maintain equivalence.
-
Forgetting to simplify fractions: Leaving fractions in non-simplified form can make calculations more complex and obscure the true value.
-
Misunderstanding the concept of GCD: Accurately finding the GCD is essential for simplifying fractions correctly.
-
Incorrectly applying equivalent fraction rules to addition and subtraction: Equivalent fractions are important in addition and subtraction, but one must not confuse the processes of simplification and finding a common denominator.
Practice Problems
To solidify your understanding, try these practice problems:
- Find three fractions equivalent to 3/8.
- Simplify the fraction 24/64.
- Determine which fraction is larger: 3/8 or 5/12 (Hint: find a common denominator).
- Convert 3/8 to a decimal and a percentage.
- If a recipe calls for 3 cups of sugar for every 8 cups of flour, how much sugar is needed if you use 16 cups of flour?
Conclusion
Mastering the concept of equivalent fractions is a crucial step in building a strong mathematical foundation. This in-depth guide has explored various aspects of fractions equivalent to 3/8, covering different methods for finding equivalents, simplifying fractions, visualizing the concept, and highlighting practical applications. By understanding and applying these principles, you'll be better equipped to tackle more complex mathematical problems and excel in various academic and real-world scenarios. Remember to practice regularly, focusing on understanding the underlying concepts rather than simply memorizing procedures. With consistent effort, you can confidently navigate the world of equivalent fractions and unlock a deeper understanding of mathematical principles.
Latest Posts
Latest Posts
-
Number Of Valence Electrons In Ar
Apr 02, 2025
-
What Is 5 9 In Decimal Form
Apr 02, 2025
-
How Many Grams In 8 Kilograms
Apr 02, 2025
-
12x 4y 20 Solve For Y
Apr 02, 2025
-
Most Reactive Group On The Periodic Table
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Fractions That Are Equivalent To 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
