Find The Slope Of The Line Perpendicular
listenit
Apr 03, 2025 · 5 min read
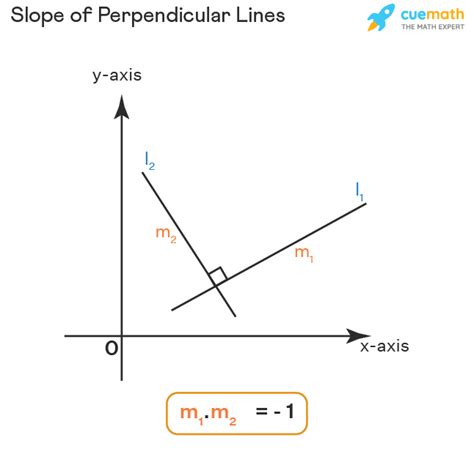
Table of Contents
Finding the Slope of a Perpendicular Line: A Comprehensive Guide
Understanding the relationship between slopes of perpendicular lines is crucial in various mathematical and real-world applications. This comprehensive guide will delve into the concept of perpendicular lines, explore the formula for calculating the slope of a perpendicular line, and work through numerous examples to solidify your understanding. We'll also touch upon the implications and applications of this concept in different fields.
What are Perpendicular Lines?
Perpendicular lines are two lines that intersect at a right angle (90 degrees). This intersection creates four right angles. Visually, imagine the shape of a plus sign (+); the lines forming that plus sign are perpendicular to each other. The key characteristic that distinguishes perpendicular lines is their slopes.
The Relationship Between Slopes of Perpendicular Lines
The relationship between the slopes of two perpendicular lines is the cornerstone of understanding how to find the slope of a perpendicular line. The slopes are negative reciprocals of each other. This means that if you know the slope of one line, you can easily determine the slope of the line perpendicular to it.
Let's break this down:
-
Reciprocal: The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 3/4 is 4/3.
-
Negative: This means we change the sign of the reciprocal. If the slope is positive, the slope of the perpendicular line will be negative, and vice-versa.
Therefore, if the slope of line m is m1, and the slope of the line perpendicular to it is m2, the relationship is expressed as:
m2 = -1/m1
or
m1 * m2 = -1
Calculating the Slope of a Perpendicular Line: Step-by-Step Guide
Let's walk through the process of calculating the slope of a perpendicular line with several examples.
Step 1: Find the slope of the given line. This often involves using the slope formula:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
Step 2: Find the reciprocal of the slope. Invert the fraction. If the slope is an integer, consider it as a fraction with a denominator of 1 (e.g., 3 becomes 3/1).
Step 3: Change the sign. Make the reciprocal negative if it was positive, and positive if it was negative.
Example 1: A line with a slope of 2
-
Given slope (m1): 2
-
Reciprocal: 1/2
-
Negative reciprocal (m2): -1/2
Therefore, the slope of the line perpendicular to a line with a slope of 2 is -1/2.
Example 2: A line with a slope of -3/4
-
Given slope (m1): -3/4
-
Reciprocal: -4/3
-
Negative reciprocal (m2): 4/3
Therefore, the slope of the line perpendicular to a line with a slope of -3/4 is 4/3.
Example 3: A line passing through points (1, 2) and (4, 6)
-
Find the slope of the given line:
m1 = (6 - 2) / (4 - 1) = 4/3
-
Reciprocal: 3/4
-
Negative reciprocal (m2): -3/4
Therefore, the slope of the line perpendicular to the line passing through (1,2) and (4,6) is -3/4.
Example 4: A horizontal line (slope = 0)
A horizontal line has a slope of 0. The reciprocal of 0 is undefined. However, a line perpendicular to a horizontal line is a vertical line, which has an undefined slope.
Example 5: A vertical line (undefined slope)
A vertical line has an undefined slope. A line perpendicular to a vertical line is a horizontal line, which has a slope of 0.
Special Cases and Considerations
-
Undefined Slopes: Remember that vertical lines have undefined slopes. A line perpendicular to a vertical line will always be horizontal, and have a slope of 0.
-
Zero Slopes: Horizontal lines have a slope of 0. A line perpendicular to a horizontal line will be vertical, having an undefined slope.
-
Negative Slopes: Pay close attention to signs. The negative reciprocal involves changing the sign after taking the reciprocal.
Applications of Perpendicular Lines and Slopes
The concept of perpendicular lines and their slopes isn't just a theoretical exercise; it has numerous practical applications across various fields:
-
Geometry: Constructing perpendicular bisectors, finding altitudes of triangles, determining the relationship between lines and shapes.
-
Computer Graphics: Creating right angles in computer-aided design (CAD) software, generating realistic 3D models.
-
Physics: Analyzing forces acting at right angles, calculating velocity components, determining trajectories.
-
Engineering: Designing structures with supporting beams at right angles, ensuring stability in construction.
-
Mapping and Surveying: Determining distances and angles using right-angled triangles, creating accurate maps.
-
Calculus: Finding tangents and normals to curves, which often involve perpendicular lines.
Advanced Concepts and Further Exploration
While this guide provides a solid foundation, further exploration into related mathematical concepts can enhance your understanding. These include:
-
Vectors: Understanding vectors and their dot products offers an alternative way to determine perpendicularity. When the dot product of two vectors is zero, they are perpendicular.
-
Linear Algebra: Matrix operations provide powerful tools for working with systems of linear equations, which are inherently linked to the concept of lines and their slopes.
-
Analytic Geometry: This branch of mathematics deeply explores the relationship between algebra and geometry, providing a more rigorous framework for understanding lines, slopes, and perpendicularity.
Conclusion: Mastering Perpendicular Line Slopes
Finding the slope of a perpendicular line is a fundamental concept in mathematics with wide-ranging applications. By mastering the technique of finding the negative reciprocal, you unlock the ability to solve numerous problems and gain a deeper understanding of the geometry of lines and their interactions. Remember the key relationship: the slopes of perpendicular lines are negative reciprocals of each other. Practice the examples provided and explore the advanced concepts mentioned to solidify your understanding and broaden your mathematical abilities. With consistent practice and a firm grasp of the core principles, you will be well-equipped to tackle more complex problems involving perpendicular lines.
Latest Posts
Latest Posts
-
Man Is The Only Animal That Blushes Or Needs To
Apr 04, 2025
-
In What Organelle Does Cellular Respiration Occur In
Apr 04, 2025
-
How Many Electrons Are In Bromine
Apr 04, 2025
-
Which Organelle Does Cellular Respiration Occur In
Apr 04, 2025
-
Lewis Structure For N Ch3 3
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Slope Of The Line Perpendicular . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
