Common Multiples Of 9 And 7
listenit
Apr 01, 2025 · 5 min read
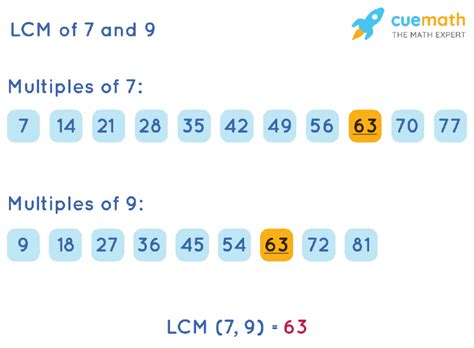
Table of Contents
Delving into the World of Common Multiples: A Deep Dive into Multiples of 9 and 7
Finding common multiples, especially for seemingly simple numbers like 9 and 7, can seem straightforward at first glance. However, a deeper exploration reveals fascinating patterns and connections within the realm of number theory. This article will provide a comprehensive understanding of common multiples of 9 and 7, exploring various methods for finding them, their significance in mathematics, and real-world applications. We’ll move beyond simple calculations and delve into the underlying mathematical principles, ensuring a thorough understanding of this fundamental concept.
Understanding Multiples
Before we dive into the specifics of common multiples of 9 and 7, let's establish a clear understanding of what multiples are. A multiple of a number is the product of that number and any integer (whole number). For instance:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, and so on.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, and so on.
Notice how the multiples of each number extend infinitely in both positive and negative directions. We're primarily concerned with positive multiples in most practical applications.
Identifying Common Multiples
A common multiple is a number that is a multiple of two or more numbers. In our case, we're interested in the common multiples of 9 and 7. Looking at the lists above, we can already spot one: 63. But how do we find more, and is there a systematic way to do this? Yes, there are several methods:
Method 1: Listing Multiples
The simplest method, though not always the most efficient for larger numbers, is to list the multiples of each number until we find common ones. While effective for small numbers like 9 and 7, this method becomes cumbersome when dealing with larger numbers or needing to find many common multiples.
Method 2: Prime Factorization
This method is more efficient and provides a deeper understanding of the underlying mathematical principles. We start by finding the prime factorization of each number:
- 9 = 3 x 3 = 3²
- 7 = 7 (7 is a prime number)
To find the least common multiple (LCM), we take the highest power of each prime factor present in the factorizations and multiply them together:
- LCM(9, 7) = 3² x 7 = 63
The LCM is the smallest positive number that is a multiple of both 9 and 7. All other common multiples will be multiples of the LCM. Therefore, the common multiples of 9 and 7 are: 63, 126, 189, 252, 315, and so on. Each subsequent common multiple is obtained by adding 63 to the previous one.
Method 3: Using the Formula
A formula exists for finding the LCM of two numbers, 'a' and 'b':
LCM(a, b) = (|a x b|) / GCD(a, b)
Where GCD(a, b) is the greatest common divisor of 'a' and 'b'. The GCD of 9 and 7 is 1 (as they are coprime, meaning they share no common factors other than 1). Therefore:
LCM(9, 7) = (9 x 7) / 1 = 63
This formula provides a direct calculation of the LCM, avoiding the need for listing multiples or extensive prime factorization, particularly useful when working with larger numbers.
Significance and Applications of Common Multiples
Understanding common multiples isn't just an academic exercise; it has numerous applications across various fields:
Scheduling and Timing
Common multiples are crucial in scheduling tasks that need to occur at regular intervals. Imagine two machines operating on a cycle: one every 9 minutes and the other every 7 minutes. To determine when both machines will be idle simultaneously, we need to find the common multiples of 9 and 7. The first time they are both idle is after 63 minutes.
Measurement and Conversions
Common multiples help in situations where conversions between different units are required. For instance, converting between inches and centimeters might involve finding common multiples of the conversion factor.
Pattern Recognition
Identifying common multiples facilitates pattern recognition in various mathematical and scientific contexts. Recurring patterns in sequences or cyclical phenomena often relate to common multiples.
Music Theory
Common multiples play a role in music theory, particularly in determining harmonious intervals and chord progressions. The relationships between different musical notes are often expressed using ratios, and common multiples can be used to simplify these ratios.
Exploring Further: Beyond the Basics
Our exploration of common multiples of 9 and 7 has only scratched the surface. Several avenues warrant further investigation:
Finding the nth Common Multiple
While finding the first few common multiples is relatively straightforward, determining the nth common multiple requires a more structured approach. This often involves using the formula for arithmetic sequences, where the common difference is the LCM.
Extending to More Than Two Numbers
The concepts discussed can be extended to finding common multiples of three or more numbers. The prime factorization method and LCM calculations can be adapted accordingly, though the complexity increases with the number of numbers involved.
Applications in Advanced Mathematics
Common multiples have deeper applications in areas like abstract algebra and number theory, contributing to concepts like modular arithmetic and group theory.
Computational Methods
For very large numbers, computational methods and algorithms are necessary for efficiently finding common multiples. Computer programs and specialized software can handle these calculations with greater speed and accuracy.
Conclusion: The Enduring Relevance of Common Multiples
The seemingly simple concept of common multiples of 9 and 7 opens a window into a rich world of mathematical principles and applications. From scheduling to music theory, the ability to identify and understand common multiples proves invaluable in various contexts. This article has explored different approaches to finding these multiples, highlighting their significance and encouraging further exploration into the fascinating realm of number theory. The more we delve into the intricacies of mathematics, the more we appreciate the interconnectedness and elegance of its fundamental concepts. The study of common multiples, even in the context of seemingly simple numbers like 9 and 7, provides a robust foundation for understanding more complex mathematical ideas. It’s a testament to the enduring power of fundamental mathematical principles in solving real-world problems and driving innovation across diverse fields.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 18 And 30
Apr 02, 2025
-
Miles Per Hour To Meters Per Minute
Apr 02, 2025
-
Has A Definite Volume And Shape
Apr 02, 2025
-
What Is 3 Out Of 25 As A Percentage
Apr 02, 2025
-
Distance From Earth To Mars In Light Years
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 9 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
