Greatest Common Factor Of 18 And 30
listenit
Apr 02, 2025 · 5 min read
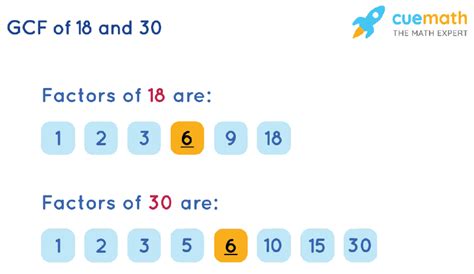
Table of Contents
Greatest Common Factor of 18 and 30: A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles unlocks a world of mathematical elegance and practical applications. This article delves deep into finding the greatest common factor of 18 and 30, exploring multiple methods and highlighting the broader significance of GCF in mathematics and beyond.
Understanding the Greatest Common Factor (GCF)
The greatest common factor, also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory, impacting various mathematical fields and real-world applications.
Why is finding the GCF important? The GCF simplifies fractions, helps solve problems involving ratios and proportions, and plays a crucial role in algebraic manipulations.
Methods for Finding the GCF
Several methods exist for determining the GCF. Let's explore the most common approaches, applying them to find the GCF of 18 and 30:
1. Listing Factors Method:
This method involves listing all the factors of each number and identifying the largest factor common to both.
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Comparing the lists, we see that the common factors are 1, 2, 3, and 6. The greatest of these is 6. Therefore, the GCF of 18 and 30 is 6.
This method works well for smaller numbers but becomes cumbersome for larger ones.
2. Prime Factorization Method:
This method utilizes the prime factorization of each number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 30: 2 x 3 x 5
To find the GCF, we identify the common prime factors and their lowest powers. Both 18 and 30 share a 2 and a 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Multiplying these together gives us 2 x 3 = 6. Therefore, the GCF of 18 and 30 is 6.
This method is more efficient for larger numbers and provides a systematic approach.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on repeated application of the division algorithm.
The steps are as follows:
- Divide the larger number (30) by the smaller number (18) and find the remainder. 30 ÷ 18 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (18) and the smaller number with the remainder (12).
- Repeat the process: 18 ÷ 12 = 1 with a remainder of 6.
- Repeat again: 12 ÷ 6 = 2 with a remainder of 0.
When the remainder is 0, the last non-zero remainder is the GCF. In this case, the GCF is 6.
The Euclidean algorithm is computationally efficient and forms the basis for many advanced mathematical algorithms.
Applications of the Greatest Common Factor
The GCF's utility extends far beyond simple arithmetic exercises. Here are some key applications:
1. Simplifying Fractions:
Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. For example, the fraction 18/30 can be simplified by dividing both the numerator and the denominator by their GCF, which is 6: 18/30 = (18 ÷ 6) / (30 ÷ 6) = 3/5.
2. Solving Ratio and Proportion Problems:
GCF helps simplify ratios and proportions. If two quantities are in the ratio 18:30, simplifying this ratio using the GCF (6) gives us the equivalent ratio 3:5. This simplifies understanding and working with the relationship between the quantities.
3. Algebraic Simplification:
The GCF is essential in factoring algebraic expressions. Finding the GCF of the terms in an expression allows us to factor it, simplifying the expression and making it easier to solve equations or analyze its properties.
4. Geometric Problems:
GCF is used to solve problems related to area and perimeter calculations. For instance, finding the largest square tile that can perfectly cover a rectangular floor of dimensions 18 units by 30 units requires finding the GCF of 18 and 30. The answer, 6 units, determines the size of the largest square tile that will fit without any cuts or gaps.
5. Cryptography and Number Theory:
The GCF, particularly the Euclidean algorithm, plays a significant role in modern cryptography. Algorithms like RSA encryption rely on the properties of GCF and prime numbers for their security.
6. Computer Science and Algorithm Design:
GCF algorithms are crucial in various computer science applications. They're used in tasks like data compression, image processing, and optimizing computer programs. The efficiency of the Euclidean algorithm makes it a preferred choice in these applications.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to exploring related concepts in number theory:
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more numbers. The GCF and LCM are closely related; the product of the GCF and LCM of two numbers is equal to the product of the two numbers. For 18 and 30, the LCM is 90.
-
Modular Arithmetic: The concept of congruence modulo n (written as a ≡ b (mod n)) is fundamental in number theory and cryptography. The GCF plays a crucial role in solving congruences.
-
Diophantine Equations: These equations involve finding integer solutions. The GCF is often used to determine the existence and the number of solutions to linear Diophantine equations.
Conclusion: The Enduring Significance of the GCF
The seemingly simple task of finding the greatest common factor of 18 and 30 reveals a deeper mathematical elegance and practical utility. From simplifying fractions to securing online transactions, the GCF and its related concepts form the bedrock of many mathematical applications and fields. Understanding the various methods for finding the GCF, along with its broader significance, enhances one's mathematical literacy and appreciation for the interconnectedness of mathematical ideas. The exploration of GCF goes beyond a simple arithmetic exercise; it's a journey into the heart of number theory and its remarkable applications in the world around us. By grasping these fundamental concepts, we unlock a richer understanding of the mathematical world and its impact on our lives.
Latest Posts
Latest Posts
-
How Many Feet Is 1 2 Miles
Apr 03, 2025
-
How Many Pounds In One Pint
Apr 03, 2025
-
Compute And Interpret The Mean Of The Random Variable X
Apr 03, 2025
-
Where Does Carbon Dioxide Enter A Plant
Apr 03, 2025
-
Does The Period Come Before Or After The Quote
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 18 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
