Common Multiples Of 7 And 9
listenit
Mar 25, 2025 · 5 min read
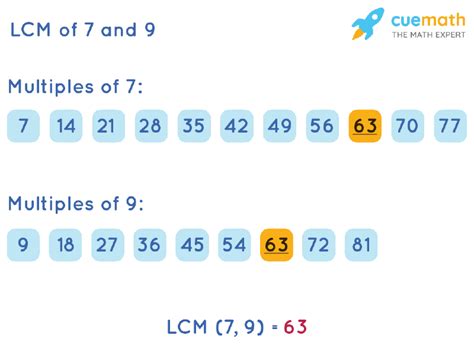
Table of Contents
Unlocking the Secrets of Common Multiples: A Deep Dive into Multiples of 7 and 9
Finding common multiples, especially for numbers like 7 and 9, might seem like a daunting task at first glance. However, understanding the underlying mathematical principles and employing efficient strategies can transform this challenge into an engaging exploration of number theory. This comprehensive guide will delve into the fascinating world of common multiples, focusing specifically on 7 and 9, equipping you with the knowledge and tools to master this concept.
Understanding Multiples
Before we dive into the specifics of common multiples of 7 and 9, let's solidify our understanding of multiples themselves. A multiple of a number is simply the product of that number and any integer (whole number). For instance:
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, and so on. Notice that each number is obtained by multiplying 7 by a different whole number (1, 2, 3, 4, etc.).
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, and so on. Similarly, these are obtained by multiplying 9 by different whole numbers.
What are Common Multiples?
A common multiple is a number that is a multiple of two or more numbers. In the context of 7 and 9, a common multiple is a number that appears in both the list of multiples of 7 and the list of multiples of 9. For example, 63 is a common multiple of 7 and 9 because:
- 63 = 7 x 9
- 63 = 9 x 7
Finding the Least Common Multiple (LCM)
Among the infinite number of common multiples for any given set of numbers, the least common multiple (LCM) holds particular significance. It's the smallest positive integer that is a multiple of all the numbers in the set. Finding the LCM is often a crucial step in solving various mathematical problems, including simplifying fractions and solving problems related to cycles and periodic events.
There are several methods to determine the LCM of 7 and 9:
Method 1: Listing Multiples
The most straightforward approach, albeit time-consuming for larger numbers, is to list the multiples of each number until you find the smallest common one.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
As you can see, the smallest number appearing in both lists is 63. Therefore, the LCM of 7 and 9 is 63.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical structure. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 7: 7 (7 is a prime number itself)
- Prime factorization of 9: 3² (9 = 3 x 3)
Since 7 and 3 are distinct prime numbers, the LCM is simply the product of their highest powers: 7 x 3² = 7 x 9 = 63.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, the LCM can be calculated using the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where GCD(a, b) represents the greatest common divisor (GCD) of a and b.
- The GCD of 7 and 9 is 1 (they share no common factors other than 1).
- LCM(7, 9) = (7 x 9) / 1 = 63
Beyond the LCM: Exploring Other Common Multiples
While the LCM is the smallest common multiple, there are infinitely many other common multiples. These can be found by multiplying the LCM by any positive integer. For 7 and 9:
- 63 x 1 = 63
- 63 x 2 = 126
- 63 x 3 = 189
- 63 x 4 = 252
- ...and so on.
Therefore, the set of common multiples of 7 and 9 is {63, 126, 189, 252, 315, ...}. This sequence continues indefinitely.
Applications of Common Multiples
The concept of common multiples, especially the LCM, finds applications in various real-world scenarios:
-
Scheduling: Imagine two buses departing from the same station, one every 7 minutes and the other every 9 minutes. The LCM (63 minutes) determines when they will depart simultaneously again.
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions with unlike denominators.
-
Cyclic Patterns: Problems involving repeating patterns or cycles often require finding the LCM to determine when the patterns will coincide. Think about gears in a machine or the phases of the moon.
-
Measurement Conversions: Converting between different units of measurement sometimes involves using the LCM to find a common denominator.
Common Multiples in Advanced Mathematics
The concept of common multiples extends beyond basic arithmetic and finds its way into more advanced mathematical fields:
-
Abstract Algebra: The concept of least common multiples is generalized in abstract algebra, dealing with more complex algebraic structures.
-
Number Theory: The study of LCMs contributes to understanding the properties of integers and their relationships.
-
Modular Arithmetic: The LCM plays a vital role in modular arithmetic, a branch of number theory dealing with remainders after division.
Conclusion: Mastering Common Multiples
Understanding common multiples, particularly for numbers like 7 and 9, is a fundamental skill in mathematics. This guide has provided a comprehensive overview, from the basic definitions to the practical applications and advanced mathematical connections. By employing the methods described—listing multiples, prime factorization, or the formula—you can efficiently determine the LCM and other common multiples. Remember that the LCM is just the starting point; there are infinitely many common multiples awaiting discovery. With a firm grasp of these concepts, you'll be well-equipped to tackle various mathematical challenges and appreciate the beauty and elegance of number theory. The journey into the world of numbers is a continuous one, and understanding common multiples is a crucial stepping stone on that path.
Latest Posts
Latest Posts
-
Is 5 7 A Rational Number
Mar 28, 2025
-
How To Find The Perpendicular Slope
Mar 28, 2025
-
120 In Equals How Many Feet
Mar 28, 2025
-
How To Find Real Zeros Of A Polynomial
Mar 28, 2025
-
What Prevents Speciation From Occurring In Sympatric Populations
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
