Are All Sides Of A Rhombus Congruent
listenit
Mar 26, 2025 · 6 min read
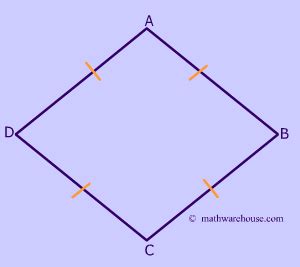
Table of Contents
Are All Sides of a Rhombus Congruent? A Deep Dive into Rhombus Properties
The question, "Are all sides of a rhombus congruent?" is a fundamental one in geometry, particularly when dealing with quadrilaterals. The answer, simply put, is yes. This seemingly straightforward answer, however, opens the door to a deeper exploration of the rhombus's properties, its relationship to other quadrilaterals, and its applications in various fields. This comprehensive article will delve into the intricacies of the rhombus, providing a thorough understanding of its characteristics and proving the congruency of its sides.
Understanding the Rhombus: Definition and Key Properties
Before proving the congruency of a rhombus's sides, let's establish a clear understanding of what constitutes a rhombus. A rhombus is defined as a quadrilateral with all four sides having equal length. This fundamental property distinguishes it from other quadrilaterals like squares, rectangles, and parallelograms.
While all sides being equal is the defining characteristic, a rhombus also possesses other notable properties:
- Opposite sides are parallel: This means that opposite sides of a rhombus will never intersect, no matter how far they are extended. This property is inherited from its classification as a parallelogram.
- Opposite angles are equal: Just like in parallelograms, the opposite angles of a rhombus are congruent. This means they have the same measure.
- Consecutive angles are supplementary: Any two angles that share a side (consecutive angles) add up to 180 degrees.
- Diagonals bisect each other: The diagonals of a rhombus intersect at a point that divides each diagonal into two equal segments.
- Diagonals are perpendicular bisectors: This is a crucial property. The diagonals not only bisect each other but also intersect at a right angle (90 degrees). This perpendicular intersection creates four congruent right-angled triangles within the rhombus.
Proving the Congruency of Rhombus Sides: Geometric Proof
The congruency of a rhombus's sides is not just an assertion; it's a geometric truth that can be proven using various methods. Let's explore one such proof:
Theorem: All sides of a rhombus are congruent.
Proof:
-
Consider a rhombus ABCD: Let's define a rhombus with vertices A, B, C, and D.
-
Opposite sides are parallel: By definition of a rhombus (and its classification as a parallelogram), we know that AB || DC and AD || BC.
-
Construct diagonals AC and BD: Draw the diagonals connecting opposite vertices. These diagonals intersect at a point, let's call it O.
-
Diagonals bisect each other: The diagonals of a rhombus bisect each other, meaning AO = OC and BO = OD.
-
Consider triangles ΔABO and ΔCBO: Now, focus on triangles formed by the diagonals. In ΔABO and ΔCBO:
- AB = CB (Given – all sides of a rhombus are equal)
- AO = OC (Diagonals bisect each other)
- BO = BO (Common side)
Therefore, by the Side-Side-Side (SSS) congruence postulate, ΔABO ≅ ΔCBO.
-
Congruent sides: Since ΔABO ≅ ΔCBO, their corresponding sides are congruent. This implies that AB = BC.
-
Similarly, consider other triangles: By employing similar logic and considering triangles ΔADO and ΔBDO, we can prove that AD = CD.
-
Conclusion: Since AB = BC and AD = CD, and all sides of a rhombus are equal by definition, we have definitively proven that all four sides (AB, BC, CD, DA) of a rhombus are congruent. Therefore, the statement "All sides of a rhombus are congruent" is true.
Relationship to Other Quadrilaterals: A Comparative Analysis
Understanding the rhombus necessitates comparing it to other quadrilaterals. This comparison highlights the rhombus's unique characteristics and its place within the broader family of quadrilaterals:
-
Square: A square is a special case of a rhombus where all angles are also equal (90 degrees). Therefore, a square is a rhombus, but not all rhombuses are squares.
-
Rectangle: A rectangle is a quadrilateral with four right angles. While a rhombus can have right angles (making it a square), it's not necessarily a rectangle unless it's a square. A rhombus generally does not have right angles.
-
Parallelogram: A rhombus is a type of parallelogram. Parallelograms have opposite sides that are both parallel and equal in length. However, a parallelogram doesn't necessarily have all four sides equal, which is the defining characteristic of a rhombus.
-
Kite: A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. While a rhombus satisfies this condition (with two pairs of adjacent sides being equal), a kite does not necessarily have all four sides equal.
This comparative analysis emphasizes that the rhombus occupies a specific niche within the broader classification of quadrilaterals, possessing unique properties not shared by all its relatives.
Applications of Rhombus Properties in Real World
The properties of a rhombus are not just abstract geometrical concepts; they find practical applications in various fields:
-
Engineering: The strength and stability of rhombus shapes are utilized in structural engineering. Rhombus-shaped trusses and bracing systems are common in bridges and buildings due to their ability to distribute weight efficiently.
-
Art and Design: The symmetrical and visually appealing nature of rhombuses makes them a popular element in art, design, and architecture. They are frequently incorporated into patterns, mosaics, and building facades.
-
Crystallography: The study of crystal structures often involves identifying and analyzing rhombus-shaped unit cells. The properties of rhombuses are critical in understanding the arrangement of atoms within crystals.
-
Games and Puzzles: The geometric properties of rhombuses are exploited in various games and puzzles, from tiling problems to geometric construction challenges.
-
Textiles and Fabrics: Rhombus patterns are frequently found in woven fabrics and textiles, contributing to the aesthetic appeal and texture of the materials.
Advanced Concepts and Further Exploration
Beyond the basics, there are more advanced concepts associated with rhombuses:
-
Area Calculation: The area of a rhombus can be calculated using different formulas, such as Area = ½ * d1 * d2, where d1 and d2 are the lengths of the diagonals.
-
Circumradius and Inradius: Like other geometric shapes, a rhombus has associated circumradius (radius of the circumscribed circle) and inradius (radius of the inscribed circle). Calculating these radii involves more complex geometric principles.
-
Rhombus in Higher Dimensions: The concept of a rhombus can be extended to higher dimensions, leading to the exploration of more complex geometric structures.
Conclusion: The Significance of Rhombus Congruency
The congruency of all sides of a rhombus is a fundamental and defining characteristic. This property, coupled with other unique features, distinguishes the rhombus within the broader world of quadrilaterals and grants it a significant role in various applications across diverse fields. This article has provided a comprehensive overview, demonstrating not only the truth of the statement "All sides of a rhombus are congruent" but also exploring the deeper implications of this fundamental geometric property. Understanding this property allows for a deeper appreciation of the rhombus's unique place in geometry and its practical relevance in the real world. Further exploration of the advanced concepts related to rhombuses will only enrich this understanding and reveal the continued significance of this fascinating quadrilateral.
Latest Posts
Latest Posts
-
Is 6 8 Equivalent To 3 4
Mar 29, 2025
-
Whats 1 2 Of 1 3
Mar 29, 2025
-
The Outermost Layer Of The Kidney
Mar 29, 2025
-
X 2 6x 9 0 Graph
Mar 29, 2025
-
What Is The Lcm Of 15 And 6
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Are All Sides Of A Rhombus Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
