A Quadrilateral Is Always A Rhombus
listenit
Mar 24, 2025 · 5 min read
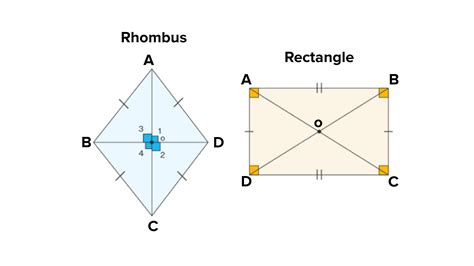
Table of Contents
- A Quadrilateral Is Always A Rhombus
- Table of Contents
- When is a Quadrilateral Always a Rhombus? Exploring the Necessary Conditions
- Understanding the Defining Characteristics of a Rhombus
- Common Misconceptions: What Doesn't Guarantee a Rhombus?
- 1. Equal Angles Only:
- 2. Parallel Opposite Sides Only:
- 3. Equal Sides and One Right Angle:
- 4. Diagonals Bisecting Each Other:
- Necessary and Sufficient Conditions for a Rhombus
- Exploring Related Shapes and Their Relationships
- The Square:
- The Rectangle:
- The Parallelogram:
- The Kite:
- Proving a Quadrilateral is a Rhombus: A Step-by-Step Approach
- Advanced Concepts and Theorems
- Real-World Applications: Where Do We See Rhombuses?
- Conclusion: Precision in Geometric Classification
- Latest Posts
- Latest Posts
- Related Post
When is a Quadrilateral Always a Rhombus? Exploring the Necessary Conditions
A rhombus, a captivating figure in the world of geometry, possesses unique properties that set it apart from other quadrilaterals. Its defining characteristic? All four sides are equal in length. While many quadrilaterals might appear to be rhombuses, the statement "a quadrilateral is always a rhombus" is fundamentally incorrect. This article delves into the precise conditions that must be met for a quadrilateral to be definitively classified as a rhombus, exploring various related shapes and theorems to illuminate this geometrical truth.
Understanding the Defining Characteristics of a Rhombus
Before exploring the conditions under which a quadrilateral can be classified as a rhombus, it’s crucial to understand what precisely defines this shape. A rhombus is a parallelogram with all four sides of equal length. This seemingly simple definition encapsulates several key properties:
-
Equal Sides: This is the most fundamental property. All four sides must be congruent (of equal length).
-
Parallel Sides: A rhombus is a type of parallelogram, meaning opposite sides are parallel.
-
Opposite Angles: Opposite angles in a rhombus are equal.
-
Adjacent Angles: Adjacent angles in a rhombus are supplementary (add up to 180 degrees).
-
Diagonals: The diagonals of a rhombus bisect each other at right angles. Furthermore, the diagonals also bisect the angles of the rhombus.
It's crucial to remember that fulfilling only some of these conditions doesn't guarantee the quadrilateral is a rhombus. All properties must be satisfied.
Common Misconceptions: What Doesn't Guarantee a Rhombus?
Many geometrical figures share some, but not all, properties of a rhombus. Let's clarify some common misconceptions:
1. Equal Angles Only:
A quadrilateral with equal angles is a rectangle. While rectangles have opposite sides parallel and equal in length, they don't necessarily have all four sides equal. A square is a special case of both a rhombus and a rectangle, possessing both equal sides and equal angles.
2. Parallel Opposite Sides Only:
A quadrilateral with only parallel opposite sides is simply a parallelogram. A parallelogram's sides may or may not be equal in length. A rhombus is a specific type of parallelogram.
3. Equal Sides and One Right Angle:
If a quadrilateral has four equal sides and one right angle, it must be a square (and therefore a rhombus). The presence of a single right angle automatically implies that all angles are right angles, due to the equal side lengths and the properties of parallelograms.
4. Diagonals Bisecting Each Other:
This property alone is characteristic of parallelograms, not just rhombuses. The diagonals of many quadrilaterals (including rectangles and squares) bisect each other, but this doesn't guarantee equal side lengths.
Necessary and Sufficient Conditions for a Rhombus
To unequivocally state that a quadrilateral is a rhombus, specific, sufficient conditions must be met. These include:
-
Four Equal Sides: This is the most straightforward and definitive condition. If all four sides of a quadrilateral are congruent, then and only then is it a rhombus.
-
Parallelogram with Two Adjacent Equal Sides: If a quadrilateral is a parallelogram (opposite sides are parallel), and two adjacent sides are equal in length, then all four sides must be equal, making it a rhombus. This is because opposite sides in a parallelogram are equal.
Exploring Related Shapes and Their Relationships
Understanding the relationship between a rhombus and other quadrilaterals is crucial for accurate classification.
The Square:
A square is a special case of a rhombus (and also a rectangle). It possesses all the properties of a rhombus (four equal sides) and the additional property of having four right angles.
The Rectangle:
A rectangle is a quadrilateral with four right angles and opposite sides equal. It's not necessarily a rhombus unless all its sides happen to be equal in length (in which case it's a square).
The Parallelogram:
A parallelogram is a quadrilateral with opposite sides parallel. A rhombus is a special type of parallelogram where all sides are equal.
The Kite:
A kite has two pairs of adjacent sides that are equal in length. Unlike a rhombus, the opposite sides of a kite are not necessarily equal or parallel.
Proving a Quadrilateral is a Rhombus: A Step-by-Step Approach
When presented with a quadrilateral, use the following steps to determine if it's a rhombus:
-
Measure the Sides: Carefully measure the lengths of all four sides. If all four sides are equal, the quadrilateral is a rhombus.
-
Check for Parallelism: Verify if opposite sides are parallel. If they are, and all sides are equal, it's a rhombus.
-
Examine the Diagonals: Observe how the diagonals intersect. If they bisect each other at right angles, it strongly suggests a rhombus (but it's not sufficient on its own).
-
Consider the Angles: If you know the angles, check if opposite angles are equal and adjacent angles are supplementary. Combined with equal side lengths, this confirms a rhombus.
Advanced Concepts and Theorems
While the basic conditions for identifying a rhombus are relatively straightforward, more advanced geometrical concepts can provide additional avenues for proof. For example, vector geometry can be used to prove congruence of sides, and trigonometry can be applied to determine angle relationships.
Real-World Applications: Where Do We See Rhombuses?
Understanding rhombuses is not just an academic exercise; they appear in numerous real-world applications:
-
Crystals: Certain crystal structures exhibit rhombic shapes.
-
Engineering: Rhombus-shaped components are used in various engineering applications due to their strength and stability.
-
Art and Design: Artists and designers frequently incorporate rhombuses in their work for aesthetic purposes.
-
Nature: Rhombus-like patterns can be observed in some natural formations.
Conclusion: Precision in Geometric Classification
The statement "a quadrilateral is always a rhombus" is incorrect. A rhombus is a specific type of quadrilateral with unique properties that must all be satisfied for definitive classification. This article has highlighted the necessary and sufficient conditions for a quadrilateral to qualify as a rhombus, emphasizing the importance of precise geometric definitions and the distinctions between related shapes. By understanding these nuances, we can accurately analyze and classify quadrilaterals in both theoretical and practical contexts. Remember, simply having some of the properties of a rhombus isn't enough—all defining characteristics must be present for a definitive classification.
Latest Posts
Latest Posts
-
What Is The Formula For Lead Iv Oxide
Mar 29, 2025
-
What Is The Formula For Copper Ii Phosphate
Mar 29, 2025
-
What Is The Reciprocal Of 3 8
Mar 29, 2025
-
Multiplication Of Even And Odd Functions
Mar 29, 2025
-
1000 Milliliters Is Equal To How Many Liters
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about A Quadrilateral Is Always A Rhombus . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
