A Car Starts From Rest And Travels For 5.0 S
listenit
Mar 25, 2025 · 6 min read
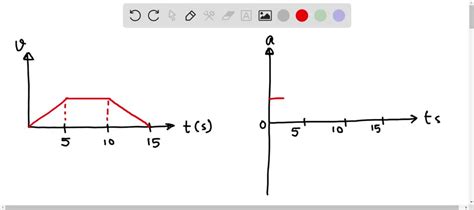
Table of Contents
A Car Starts From Rest and Travels for 5.0 s: Unpacking the Physics
A seemingly simple scenario – a car starting from rest and traveling for 5.0 seconds – actually opens a door to a wealth of physics concepts. This seemingly straightforward situation allows us to explore fundamental principles of motion, delve into the complexities of acceleration, and even touch upon the nuances of real-world driving conditions. Let's unpack this seemingly simple problem and discover the rich physics embedded within.
Understanding the Basics: Initial Conditions and Assumptions
Before we dive into the calculations, let's clearly define our initial conditions and the assumptions we'll be making. We are given that the car starts from rest. This means its initial velocity (v<sub>i</sub>) is 0 m/s. The time interval (t) is 5.0 seconds. However, to proceed further, we need to make some assumptions:
- Constant Acceleration: We'll assume, for simplicity, that the car accelerates at a constant rate. In reality, this is unlikely, as the driver will likely ease off the accelerator as they reach higher speeds. However, the constant acceleration assumption allows us to utilize straightforward kinematic equations.
- One-Dimensional Motion: We’re considering motion in a single direction (e.g., along a straight road). This simplifies the problem by eliminating the complexities of two- or three-dimensional motion.
- Negligible External Forces: We'll ignore external forces like air resistance and friction. While these are significant in real-world scenarios, neglecting them allows for a clearer understanding of the fundamental principles involved.
Applying the Kinematic Equations
With our assumptions in place, we can employ the kinematic equations of motion to analyze the car's movement. These equations relate displacement, velocity, acceleration, and time. The most relevant equations for this scenario are:
- v<sub>f</sub> = v<sub>i</sub> + at: This equation relates final velocity (v<sub>f</sub>), initial velocity (v<sub>i</sub>), acceleration (a), and time (t).
- Δx = v<sub>i</sub>t + ½at²: This equation relates displacement (Δx), initial velocity (v<sub>i</sub>), acceleration (a), and time (t).
Since the car starts from rest (v<sub>i</sub> = 0 m/s), these equations simplify to:
- v<sub>f</sub> = at
- Δx = ½at²
The Importance of Acceleration
Acceleration is the key factor determining the car's velocity and displacement. Without knowing the acceleration, we cannot fully describe the car's motion. Let's consider a few different scenarios to illustrate this:
Scenario 1: Constant Acceleration of 2 m/s²
If the car accelerates at a constant rate of 2 m/s², we can calculate its final velocity and displacement after 5.0 seconds using the simplified kinematic equations:
- v<sub>f</sub> = at = (2 m/s²)(5.0 s) = 10 m/s
- Δx = ½at² = ½(2 m/s²)(5.0 s)² = 25 m
This means that after 5.0 seconds, the car would be traveling at a speed of 10 m/s (approximately 36 km/h) and have covered a distance of 25 meters.
Scenario 2: Constant Acceleration of 5 m/s²
Increasing the acceleration to 5 m/s² significantly alters the results:
- v<sub>f</sub> = at = (5 m/s²)(5.0 s) = 25 m/s
- Δx = ½at² = ½(5 m/s²)(5.0 s)² = 62.5 m
In this case, the car would reach a velocity of 25 m/s (approximately 90 km/h) and travel 62.5 meters in 5.0 seconds. This highlights the profound impact of acceleration on the car's motion.
Scenario 3: Variable Acceleration: A More Realistic Approach
Our previous scenarios relied on the unrealistic assumption of constant acceleration. In reality, a car's acceleration will vary during the initial 5 seconds. The driver might accelerate aggressively at first, then ease off the accelerator as the car gains speed. To analyze such a scenario, we would need more detailed information about the acceleration as a function of time (a(t)). This often involves using calculus and more sophisticated techniques to determine velocity and displacement. This could involve using data from a car's onboard computer or using sensors to measure the actual acceleration profile.
Graphical Representation of Motion
The motion of the car can be effectively visualized using graphs. We can plot velocity versus time (v-t graph) and displacement versus time (x-t graph).
-
Velocity-Time Graph (v-t graph): For constant acceleration, the v-t graph is a straight line with a slope equal to the acceleration. The area under the v-t graph represents the displacement.
-
Displacement-Time Graph (x-t graph): For constant acceleration, the x-t graph is a parabola. The slope of the tangent to the curve at any point represents the instantaneous velocity at that point.
Beyond the Simplified Model: Real-World Factors
The simplified model we've been using ignores several crucial real-world factors:
-
Air Resistance: Air resistance opposes the car's motion and increases with speed. This means that the actual acceleration will decrease as the car's speed increases.
-
Rolling Resistance (Friction): Friction between the tires and the road also opposes motion, reducing acceleration.
-
Engine Characteristics: The engine's power output is not constant. The car will accelerate most rapidly at lower speeds and its acceleration will decrease as it reaches higher speeds.
-
Driver Behavior: Driver reactions and driving style will greatly influence the car's acceleration profile.
To accurately model real-world scenarios, we would need to incorporate these factors, which introduces significant complexity and often requires numerical methods or computer simulations.
Exploring Advanced Concepts
The simple scenario of a car starting from rest and traveling for 5 seconds opens doors to more advanced concepts:
-
Impulse and Momentum: The change in momentum of the car is equal to the impulse applied by the engine. Calculating the impulse would require knowledge of the force applied by the engine over time.
-
Energy Considerations: The work done by the engine is converted into kinetic energy of the car. Analyzing the energy transformations can provide additional insights into the car's motion.
-
Differential Equations: For scenarios involving variable acceleration, differential equations become necessary to accurately model the system.
Conclusion: From Simplicity to Complexity
While the initial problem appears simple, a deeper analysis reveals a wealth of physical principles. The seemingly simple scenario of a car accelerating for 5 seconds allows us to explore fundamental kinematic equations, the importance of acceleration, and the limitations of simplified models. By considering real-world factors, we appreciate the complexity of describing motion accurately and the need for more sophisticated techniques for modeling realistic situations. Understanding these concepts is crucial for anyone seeking a deeper understanding of mechanics and motion. The seemingly simple exercise lays the groundwork for more complex analyses in physics and engineering. Further exploration into these advanced concepts can lead to a far richer understanding of the physical world and the intricate details that govern even the simplest-seeming motions.
Latest Posts
Latest Posts
-
What Percent Is 1 Of 7
Mar 27, 2025
-
When Gas Exerts Pressure On Its Container The Pressure Is
Mar 27, 2025
-
X 3 2 X 1 2
Mar 27, 2025
-
60 Of What Number Is 20
Mar 27, 2025
-
Graph The Linear Equation X 4
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about A Car Starts From Rest And Travels For 5.0 S . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
