When Gas Exerts Pressure On Its Container The Pressure Is
listenit
Mar 27, 2025 · 5 min read
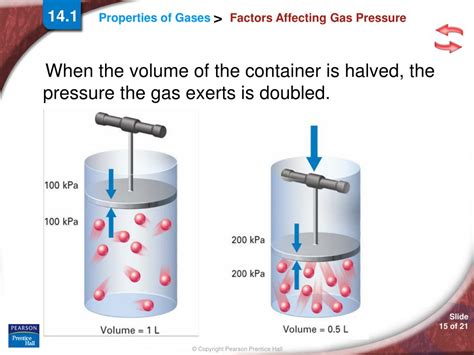
Table of Contents
When Gas Exerts Pressure on its Container, the Pressure Is… Explained
Understanding gas pressure is fundamental to comprehending many aspects of chemistry and physics. From inflating balloons to powering internal combustion engines, the pressure exerted by a gas on its container is a ubiquitous phenomenon. But what exactly is this pressure, and why does it exist? This comprehensive article delves deep into the microscopic world of gas molecules to unravel the mystery behind gas pressure and its implications.
The Kinetic Molecular Theory: The Foundation of Gas Pressure
The behavior of gases is best explained by the kinetic molecular theory (KMT). This theory postulates that gases consist of tiny particles (atoms or molecules) in constant, random motion. These particles are incredibly small compared to the distances between them, and the forces of attraction between them are negligible under normal conditions.
Key tenets of the KMT relevant to gas pressure:
- Constant, random motion: Gas particles are in perpetual motion, colliding with each other and the walls of their container. This constant bombardment is the source of gas pressure.
- Negligible intermolecular forces: The forces of attraction between gas particles are weak enough to be ignored in many cases. This allows the particles to move freely and independently.
- Elastic collisions: Collisions between gas particles and the container walls are perfectly elastic. This means that kinetic energy is conserved during these collisions; no energy is lost.
- Average kinetic energy is proportional to temperature: The average kinetic energy of gas particles is directly proportional to the absolute temperature (in Kelvin). Higher temperatures mean faster-moving particles and therefore higher pressure.
How Gas Pressure is Created: A Microscopic Perspective
Imagine a gas confined within a rigid container. The gas particles are zooming around at high speeds, constantly colliding with each other and the container walls. Each collision exerts a tiny force on the wall. The cumulative effect of billions upon billions of these tiny impacts per second generates the macroscopic pressure we measure.
Think of it like this: Imagine a swarm of tiny, energetic bees constantly buzzing against the inside walls of a beehive. Each individual bee's impact is insignificant, but the combined effect of thousands of bees constantly hitting the walls creates a significant pressure. This is analogous to the pressure exerted by gas particles on their container.
Factors Affecting Gas Pressure:
Several factors influence the magnitude of gas pressure:
- Number of particles (n): More gas particles mean more collisions with the container walls, resulting in higher pressure. This is directly proportional; doubling the number of particles doubles the pressure (at constant temperature and volume).
- Temperature (T): Higher temperatures mean faster-moving particles, leading to more forceful collisions and higher pressure. This relationship is also directly proportional; doubling the absolute temperature doubles the pressure (at constant volume and number of particles).
- Volume (V): The volume of the container influences the frequency of collisions. A smaller volume means particles collide with the walls more frequently, leading to higher pressure. This is inversely proportional; halving the volume doubles the pressure (at constant temperature and number of particles).
The Ideal Gas Law: A Mathematical Representation of Gas Pressure
The relationships between pressure, volume, temperature, and the number of particles are elegantly summarized in the ideal gas law:
PV = nRT
Where:
- P represents pressure (typically in atmospheres, Pascals, or torr).
- V represents volume (typically in liters).
- n represents the number of moles of gas.
- R is the ideal gas constant (a proportionality constant that depends on the units used for pressure, volume, and temperature).
- T represents the absolute temperature (in Kelvin).
The ideal gas law is a powerful tool for predicting and calculating gas pressure under various conditions. It provides a highly accurate approximation for many gases under normal conditions. However, it's crucial to remember that it is a model, and real gases may deviate from ideal behavior, particularly at high pressures or low temperatures.
Deviations from Ideal Gas Behavior: Real Gases
Real gases deviate from ideal gas behavior because the KMT makes some simplifying assumptions that aren't always true:
- Non-negligible intermolecular forces: At high pressures or low temperatures, the intermolecular forces between gas particles become significant. These forces can cause the particles to stick together slightly, reducing the number of collisions with the container walls and thus lowering the pressure compared to what the ideal gas law predicts.
- Finite volume of gas particles: The KMT assumes that gas particles have negligible volume compared to the volume of the container. At high pressures, the volume occupied by the gas particles themselves becomes a significant fraction of the total volume, leading to a higher pressure than predicted by the ideal gas law.
Applications of Understanding Gas Pressure
The principles of gas pressure have far-reaching applications in various fields:
Meteorology:
Understanding atmospheric pressure is crucial for weather forecasting. Changes in atmospheric pressure are associated with different weather patterns. Barometers measure atmospheric pressure, providing valuable data for weather prediction.
Automotive Engineering:
Internal combustion engines rely on the pressure of gases to generate power. The controlled combustion of fuel-air mixtures creates high pressure, which pushes pistons and drives the engine.
Deep Sea Diving:
The pressure of water increases significantly with depth. Deep-sea divers need to understand and account for this increased pressure to avoid serious health risks like decompression sickness.
Industrial Processes:
Many industrial processes involve the use of compressed gases, requiring careful control of pressure to ensure safety and efficiency.
Medical Applications:
Gas pressure plays a crucial role in medical devices such as inhalers and ventilators. Understanding gas pressure is essential for designing and operating these devices effectively.
Conclusion: Pressure is a Manifestation of Molecular Motion
Gas pressure, at its core, is a direct consequence of the constant, random motion of gas particles. The kinetic molecular theory provides a robust framework for understanding this phenomenon. The ideal gas law offers a powerful mathematical tool for predicting and calculating gas pressure, although it's crucial to be aware of its limitations and the deviations exhibited by real gases under certain conditions. The ubiquitous nature of gas pressure makes its understanding essential across a wide array of scientific and engineering disciplines. From predicting weather patterns to powering vehicles, the pressure exerted by gases on their containers is a fundamental force shaping our world.
Latest Posts
Latest Posts
-
What Is The Symbol Of Aluminum
Mar 31, 2025
-
42 Is 70 Of What Number
Mar 31, 2025
-
What Percent Of 186 Is 93
Mar 31, 2025
-
How To Find The Volume Of A Hexagonal Prism
Mar 31, 2025
-
How Much Is 64 Fl Oz
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about When Gas Exerts Pressure On Its Container The Pressure Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
