A 1 2bh Solve For H
listenit
May 09, 2025 · 5 min read
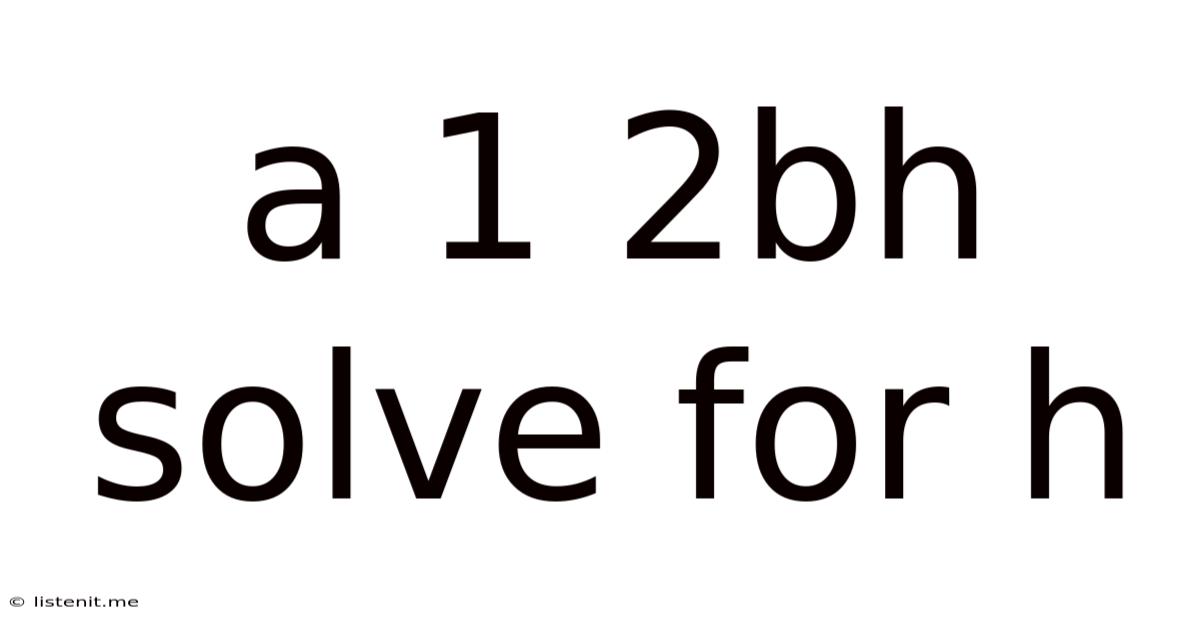
Table of Contents
Solving for 'h': A Comprehensive Guide to 1/2bh
The formula 1/2bh represents the area of a triangle, a fundamental concept in geometry and a frequently encountered calculation in various fields. Understanding how to manipulate this formula to solve for any of its variables, particularly 'h' (height), is crucial for success in mathematics and related disciplines. This comprehensive guide will delve into the intricacies of solving for 'h' in the equation A = 1/2bh, providing step-by-step solutions, real-world examples, and advanced applications.
Understanding the Components of the Formula
Before diving into the solution process, let's clarify the components of the formula A = 1/2bh:
-
A: Represents the area of the triangle. This is the quantity we're trying to find or, in our case, the quantity we already know. The area is measured in square units (e.g., square centimeters, square meters, square inches).
-
b: Represents the base of the triangle. The base is the length of one side of the triangle, usually the side that forms a horizontal line at the bottom (but not always). It's measured in linear units (e.g., centimeters, meters, inches).
-
h: Represents the height of the triangle. The height is the perpendicular distance from the base to the opposite vertex (the highest point) of the triangle. It's also measured in linear units (e.g., centimeters, meters, inches). It is crucial to remember that the height must be perpendicular to the base; otherwise, the formula will not be accurate.
Solving for 'h': A Step-by-Step Approach
To solve for 'h' in the equation A = 1/2bh, we need to isolate 'h' on one side of the equation using algebraic manipulation. Here's a step-by-step guide:
-
Multiply both sides by 2: This eliminates the fraction 1/2. The equation becomes: 2A = bh
-
Divide both sides by 'b': This isolates 'h' on one side of the equation. The final equation becomes: h = 2A/b
This simplified equation, h = 2A/b, allows us to calculate the height ('h') of a triangle if we know its area ('A') and base ('b').
Practical Applications and Examples
Let's illustrate the application of this formula with several real-world examples:
Example 1: Finding the Height of a Triangular Sail
Imagine you're a sailmaker, and you need to determine the height of a triangular sail. You know the area of the sail is 10 square meters, and its base is 5 meters. Using the formula:
h = 2A/b = (2 * 10 square meters) / 5 meters = 4 meters
Therefore, the height of the sail is 4 meters.
Example 2: Calculating the Altitude of a Triangular Plot of Land
A land surveyor needs to determine the altitude of a triangular plot of land. The plot has an area of 150 square feet and a base of 30 feet. Using the formula:
h = 2A/b = (2 * 150 square feet) / 30 feet = 10 feet
Therefore, the altitude of the triangular plot is 10 feet.
Example 3: Determining the Height of a Triangular Roof Section
A carpenter is constructing a triangular roof section. The area of the section is 24 square feet, and the base is 8 feet. To find the height:
h = 2A/b = (2 * 24 square feet) / 8 feet = 6 feet
The height of the triangular roof section is 6 feet.
Advanced Applications and Considerations
The formula A = 1/2bh and its manipulation to solve for 'h' extends beyond simple geometric calculations. It finds applications in:
-
Calculus: The formula forms the basis for calculating the area under curves using integration techniques. Understanding how to manipulate the formula is essential for understanding these more advanced concepts.
-
Engineering: Calculating the area of triangular structures is vital in civil, mechanical, and other engineering disciplines. Accurate determination of the height ('h') is critical for structural stability and design.
-
Physics: Triangular shapes appear in various physical phenomena. For instance, understanding the area of a triangular force vector can help in calculating resultant forces.
Handling Different Triangle Orientations
The formula remains the same regardless of the orientation of the triangle. The critical point is to correctly identify the base ('b') and the corresponding perpendicular height ('h'). Even if the triangle isn't oriented with its base along a horizontal axis, the principle is the same: the height is always measured perpendicular to the chosen base.
Solving for Other Variables
While this guide focuses on solving for 'h', it's important to note that the formula A = 1/2bh can also be rearranged to solve for 'A' or 'b':
-
Solving for A: The formula is already in its simplest form for calculating the area: A = 1/2bh
-
Solving for b: Divide both sides of A = 1/2bh by (1/2)h to get: b = 2A/h
Conclusion: Mastering the Fundamentals
Understanding how to solve for 'h' in the equation A = 1/2bh is a fundamental skill in mathematics and related fields. This guide has provided a clear and comprehensive explanation of the process, along with practical examples and advanced applications. By mastering this fundamental concept, you'll be well-equipped to tackle more complex problems involving triangles and their properties. Remember, accurate identification of the base and perpendicular height is crucial for obtaining accurate results. The ability to manipulate this equation is a cornerstone of mathematical proficiency and opens the door to a deeper understanding of geometry and its wider implications. Practice various problems to reinforce your understanding and build confidence in your ability to solve for 'h' and other variables in this essential geometrical formula.
Latest Posts
Latest Posts
-
1 2 3 As A Improper Fraction
May 09, 2025
-
What Is The Gcf Of 30 And 45
May 09, 2025
-
What Is The Percent Of 9 20
May 09, 2025
-
3 To The Power Of Negative 3
May 09, 2025
-
An Equilateral Triangle Is An Acute Triangle
May 09, 2025
Related Post
Thank you for visiting our website which covers about A 1 2bh Solve For H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.