What Is The Percent Of 9/20
listenit
May 09, 2025 · 5 min read
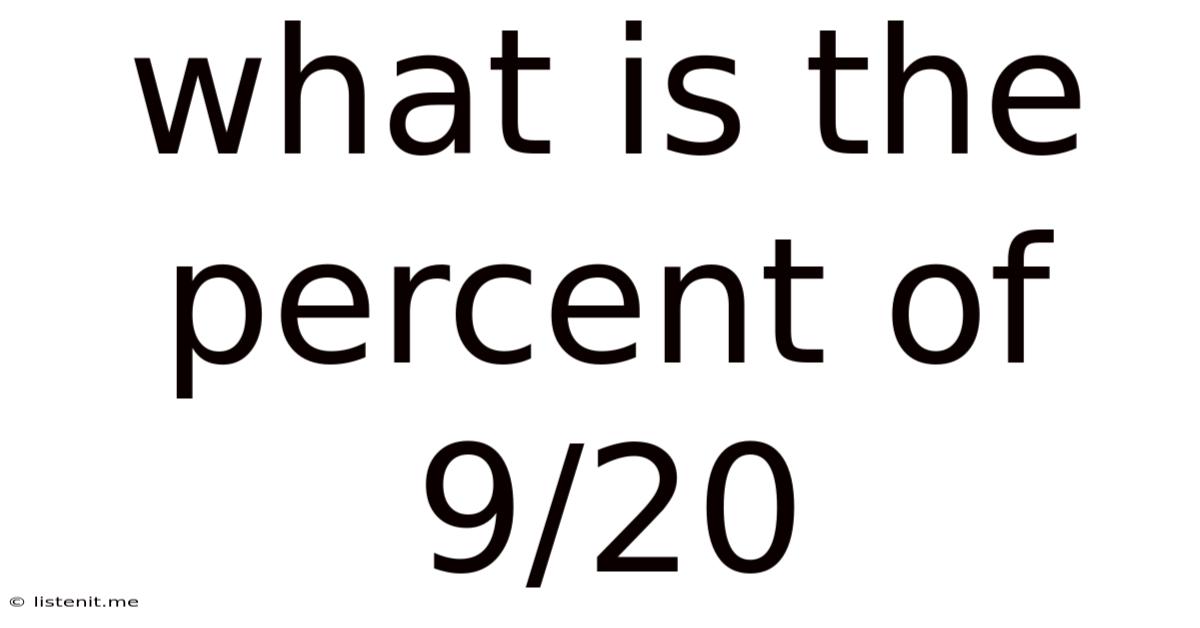
Table of Contents
What is the Percent of 9/20? A Deep Dive into Fractions, Decimals, and Percentages
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will delve into the process of converting the fraction 9/20 into a percentage, explaining the underlying concepts and offering various methods to solve similar problems. We'll also explore the broader context of fractions, decimals, and percentages and how they interrelate.
Understanding Fractions, Decimals, and Percentages
Before we dive into calculating the percentage equivalent of 9/20, let's establish a clear understanding of the three fundamental concepts: fractions, decimals, and percentages.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 9/20, 9 represents the number of parts and 20 represents the total number of equal parts.
Decimals: Expressing Fractions in Base 10
Decimals are another way to represent parts of a whole. They use a base-10 system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. Decimals are often easier to work with in calculations than fractions, particularly when using calculators or computers.
Percentages: Representing Parts per Hundred
A percentage represents a fraction or decimal as a proportion of 100. The symbol "%" indicates "per hundred." Percentages are widely used because they provide a standardized way to compare different quantities, making them easier to understand and interpret.
Calculating the Percentage Equivalent of 9/20
There are several methods to convert the fraction 9/20 into a percentage. Let's explore the most common approaches:
Method 1: Converting the Fraction to a Decimal
The simplest way to convert a fraction to a percentage is first to convert it to a decimal. This involves dividing the numerator by the denominator:
9 ÷ 20 = 0.45
Now, to convert this decimal to a percentage, simply multiply by 100:
0.45 x 100 = 45%
Therefore, 9/20 is equal to 45%.
Method 2: Using the Proportion Method
Another method involves setting up a proportion. We know that a percentage is a fraction out of 100. So, we can set up the following proportion:
9/20 = x/100
To solve for x (the percentage), we can cross-multiply:
20x = 900
x = 900 ÷ 20
x = 45
Therefore, 9/20 is equal to 45%.
Method 3: Understanding the Relationship Between Fractions and Percentages
Understanding the underlying relationship between fractions and percentages allows for a more intuitive approach. Remember that a percentage is simply a fraction with a denominator of 100. Sometimes, the fraction can be easily converted to an equivalent fraction with a denominator of 100.
While 9/20 doesn't directly simplify to a fraction with 100 as the denominator, we can manipulate it. We can multiply both the numerator and denominator by 5 to get:
(9 x 5) / (20 x 5) = 45/100
Since 45/100 means 45 out of 100, it's equal to 45%.
Real-World Applications of Percentage Calculations
Understanding how to convert fractions to percentages has numerous practical applications in daily life:
1. Calculating Discounts and Sales Tax
Imagine a store offers a 20% discount on an item. If the original price is $50, you can easily calculate the discount amount by converting 20% to a fraction (20/100 = 1/5) and multiplying it by the original price:
$50 x (20/100) = $10 discount
The final price would be $50 - $10 = $40. Similarly, sales tax calculations involve converting the tax percentage to a fraction and multiplying it by the price.
2. Analyzing Financial Statements
Percentages are crucial for interpreting financial statements. Profit margins, return on investment (ROI), and debt-to-equity ratios are all expressed as percentages, making it easier to compare performance across different periods or companies. Understanding these percentages is critical for making informed financial decisions.
3. Understanding Statistics and Data
Percentages are extensively used in presenting and interpreting statistical data. For example, survey results, election polls, and economic indicators often utilize percentages to represent proportions and trends. Being able to interpret these percentages accurately is crucial for understanding the implications of the data.
4. Calculating Grades and Scores
Many academic assessments use percentages to represent grades and scores. For instance, achieving 80% on a test means you answered 80 out of 100 questions correctly. Understanding how to calculate percentages is essential for tracking your academic progress and performance.
5. Comparing Quantities
Percentages are a useful tool for comparing quantities with different base values. For example, comparing the growth rates of two businesses with different initial sales figures is easier with percentage change calculations. The percentage change reveals the relative growth, irrespective of the initial size of the quantities.
Beyond 9/20: Practicing Percentage Conversions
Understanding how to convert 9/20 to a percentage is a stepping stone to mastering percentage calculations. To solidify your understanding, try converting other fractions to percentages:
- 1/4: This is a simple fraction that easily converts to 25%.
- 3/5: This can be converted by first finding an equivalent fraction with a denominator of 100.
- 7/8: This requires division to convert to a decimal, then multiplication by 100 to obtain the percentage.
- 17/25: This fraction can be easily converted to a percentage by multiplying both the numerator and denominator by 4.
- 2/3: This fraction will result in a recurring decimal and will need rounding to a suitable number of decimal places when converting it to a percentage.
By practicing with various fractions, you will build confidence and proficiency in converting between fractions, decimals, and percentages. Remember, this skill is invaluable in various aspects of life, from everyday calculations to complex financial analysis. The key is to understand the underlying principles and to practice consistently.
Latest Posts
Latest Posts
-
15 Degrees Celsius Equals What In Fahrenheit
May 10, 2025
-
For Every Atom Of Carbon In A Carbohydrate
May 10, 2025
-
Distinguish Among A Suspension A Colloid And A Solution
May 10, 2025
-
What Is The Difference Between Foliated And Nonfoliated Metamorphic Rock
May 10, 2025
-
Can A Right Triangle Have An Obtuse Angle
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 9/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.