What Is The Gcf Of 30 And 45
listenit
May 09, 2025 · 5 min read
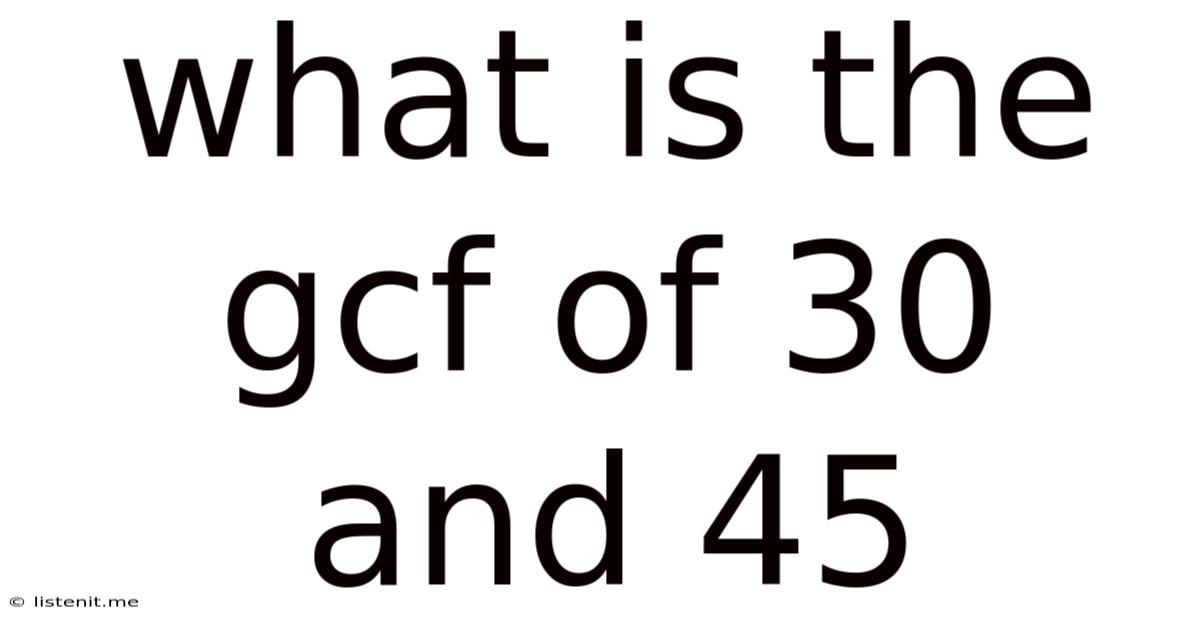
Table of Contents
What is the GCF of 30 and 45? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens up a world of mathematical understanding. This article will explore the GCF of 30 and 45 in detail, explaining various approaches and highlighting the broader significance of this fundamental concept in mathematics.
Understanding Greatest Common Factors (GCF)
Before we delve into the specifics of 30 and 45, let's establish a solid understanding of what a greatest common factor actually is. The GCF, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Think of it like finding the biggest shared building block of two numbers. Just as we can break down a complex structure into smaller components, we can break down numbers into their prime factors, revealing their GCF.
Why is the GCF Important?
Understanding GCFs is crucial for a variety of mathematical operations and real-world applications. Some key applications include:
- Simplifying Fractions: Finding the GCF allows you to simplify fractions to their lowest terms. For instance, if you have the fraction 30/45, finding the GCF helps reduce it to its simplest form.
- Solving Algebraic Equations: GCFs play a vital role in factoring polynomials and simplifying algebraic expressions.
- Measurement and Geometry: GCFs are essential when dealing with problems involving common measurements or dividing objects into equal parts. Imagine needing to cut ribbons of length 30cm and 45cm into the largest possible equal pieces without any waste – finding the GCF provides the solution.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the GCF. It involves breaking down each number into its prime factors and then identifying the common factors. Prime factors are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's apply this to 30 and 45:
1. Prime Factorization of 30:
30 = 2 x 3 x 5
2. Prime Factorization of 45:
45 = 3 x 3 x 5 = 3² x 5
3. Identifying Common Factors:
Both 30 and 45 share the prime factors 3 and 5.
4. Calculating the GCF:
The GCF is the product of the common prime factors: 3 x 5 = 15
Therefore, the greatest common factor of 30 and 45 is 15.
Method 2: Listing Factors
This method is straightforward, especially for smaller numbers. You list all the factors of each number and then identify the largest factor common to both.
1. Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
2. Factors of 45: 1, 3, 5, 9, 15, 45
3. Common Factors: 1, 3, 5, 15
4. Greatest Common Factor: 15
Again, the GCF of 30 and 45 is 15. This method is simple and easily visualized but becomes less efficient as the numbers get larger.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply it to 30 and 45:
1. Start with the larger number (45) and the smaller number (30):
45 and 30
2. Subtract the smaller number from the larger number:
45 - 30 = 15
3. Replace the larger number with the result (15) and repeat:
15 and 30
4. Subtract the smaller number from the larger number:
30 - 15 = 15
5. The numbers are now equal, indicating the GCF:
15 and 15
The GCF of 30 and 45 is 15. The Euclidean algorithm offers a systematic and efficient approach, especially useful when dealing with larger numbers where listing factors becomes impractical.
Applying the GCF: Simplifying Fractions
Let's demonstrate the practical application of finding the GCF by simplifying the fraction 30/45. Since we've determined that the GCF of 30 and 45 is 15, we can simplify the fraction as follows:
30/45 = (30 ÷ 15) / (45 ÷ 15) = 2/3
The fraction 30/45 has been successfully simplified to its lowest terms, 2/3. This simplification makes calculations easier and provides a clearer representation of the fraction's value.
Beyond 30 and 45: Extending the Concepts
While this article focuses on finding the GCF of 30 and 45, the principles discussed apply universally. You can use any of the three methods – prime factorization, listing factors, or the Euclidean algorithm – to find the GCF of any two (or more) integers.
Consider the following examples to practice your skills:
- Find the GCF of 72 and 96: Try applying each of the three methods to solidify your understanding.
- Find the GCF of 120, 180, and 240: Extending the prime factorization method to three or more numbers involves identifying the common prime factors among all the numbers.
- Use the Euclidean Algorithm for large numbers: Test its efficiency by finding the GCF of 252 and 378.
Conclusion: Mastering GCFs – A Foundation for Further Learning
Understanding the concept of the greatest common factor and mastering the methods for calculating it is not just about solving basic arithmetic problems. It forms a crucial foundation for more advanced mathematical concepts such as algebra, number theory, and even cryptography. By grasping these fundamental principles, you equip yourself with essential tools for tackling a wide range of mathematical challenges and real-world applications. The ability to efficiently find the GCF of numbers is a valuable skill that will continue to serve you well throughout your mathematical journey. Remember to practice regularly and explore different approaches to find the method that best suits your learning style and the specific problem at hand. The journey of mathematical exploration is continuous, and mastering fundamental concepts like GCFs provides a robust platform for future learning and discovery.
Latest Posts
Latest Posts
-
How Do You Find Number Of Protons In An Element
May 10, 2025
-
What Is The Difference Between Diameter And Radius
May 10, 2025
-
Evaluate Integral In Terms Of Area
May 10, 2025
-
What Would Happen If Dna Replication Did Not Occur
May 10, 2025
-
Which Particles Account For The Mass Of The Atom
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 30 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.