6 As A Percentage Of 25
listenit
May 24, 2025 · 5 min read
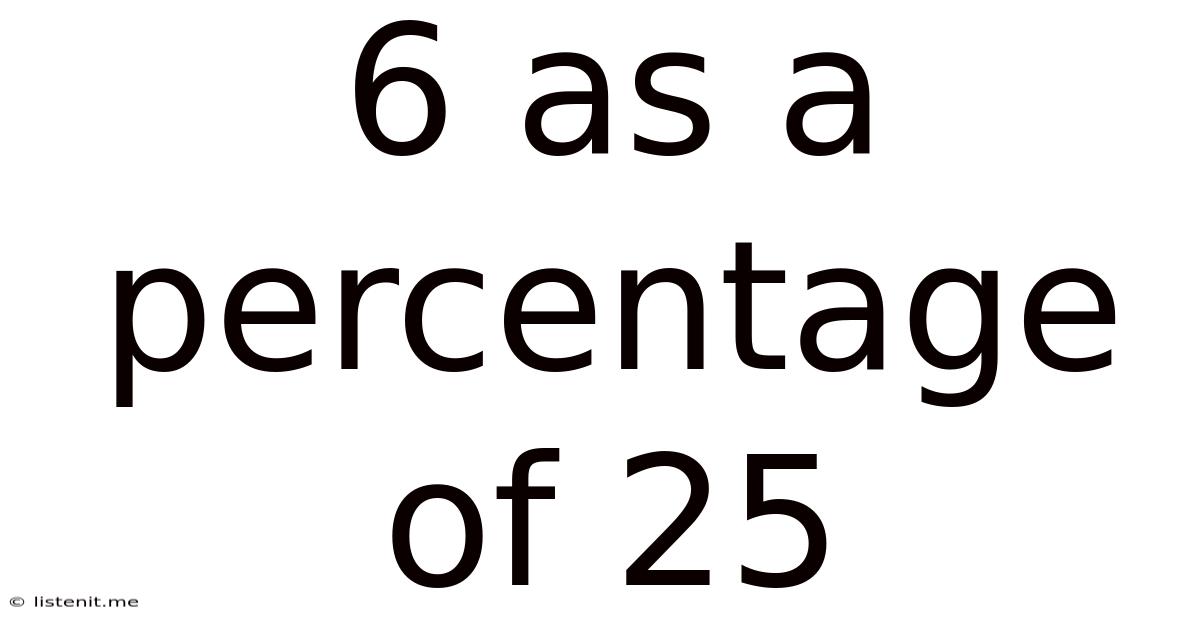
Table of Contents
6 as a Percentage of 25: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various fields, from finance and business to everyday life. Understanding how to determine one number as a percentage of another is crucial for interpreting data, making informed decisions, and solving numerous practical problems. This comprehensive guide delves into the calculation of 6 as a percentage of 25, explaining the process step-by-step, exploring different methods, and highlighting real-world applications.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: The Fraction Method
The most straightforward approach to calculating 6 as a percentage of 25 is using the fraction method. We express the relationship between 6 and 25 as a fraction:
6/25
To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. We can achieve this by multiplying both the numerator and the denominator by the same number. Since 25 multiplied by 4 equals 100, we multiply both parts of the fraction by 4:
(6 x 4) / (25 x 4) = 24/100
Now that we have a fraction with a denominator of 100, we can directly express it as a percentage:
24/100 = 24%
Therefore, 6 is 24% of 25.
Method 2: The Decimal Method
Another common method involves using decimals. We begin by expressing the relationship between 6 and 25 as a fraction:
6/25
Next, we convert this fraction to a decimal by dividing the numerator (6) by the denominator (25):
6 ÷ 25 = 0.24
To convert this decimal to a percentage, we multiply it by 100:
0.24 x 100 = 24
Adding the percentage symbol, we get:
24%
This confirms that 6 is 24% of 25.
Method 3: Using Proportions
The concept of proportions provides a powerful alternative method. A proportion is a statement that two ratios are equal. We can set up a proportion to solve this problem:
6/25 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
6 x 100 = 25 x x
600 = 25x
Now, we divide both sides by 25:
x = 600/25
x = 24
Therefore, x = 24%.
Real-World Applications: Illustrative Examples
The ability to calculate percentages finds extensive use in various real-world scenarios. Let's explore some illustrative examples where understanding "6 as a percentage of 25" proves beneficial:
1. Sales and Discounts
Imagine a store offering a discount. If an item originally costs $25 and is reduced by $6, what is the percentage discount? Using our calculation, the discount is 24%. This knowledge allows customers to easily assess the value of the discount and make informed purchasing decisions.
2. Grade Calculations
Suppose a student scores 6 points out of a possible 25 on a quiz. The student's score is 24%. This percentage allows for easy comparison with other students' scores and facilitates effective performance evaluation.
3. Financial Analysis
In financial analysis, understanding percentages is critical. If a company's profit is $6 million out of a total revenue of $25 million, the profit margin is 24%. This information is invaluable for assessing a company's profitability and financial health.
4. Survey Results
Consider a survey with 25 respondents, where 6 respondents answered "yes" to a particular question. The percentage of "yes" responses is 24%. This allows for a clear interpretation of the survey results and insights into public opinion.
5. Sports Statistics
In sports, percentages play a significant role in performance evaluation. If a basketball player makes 6 out of 25 shots, their shooting percentage is 24%. This metric offers a concise summary of the player's accuracy.
Expanding the Concept: Variations and Extensions
While this guide focuses on calculating 6 as a percentage of 25, the underlying principles can be applied to calculate any number as a percentage of another. The same methods—the fraction method, the decimal method, and the proportion method—can be used to solve various percentage problems.
For instance, if you want to calculate 12 as a percentage of 50, you would follow the same steps:
- Fraction method: 12/50 = (12 x 2)/(50 x 2) = 24/100 = 24%
- Decimal method: 12 ÷ 50 = 0.24 x 100 = 24%
- Proportion method: 12/50 = x/100 => 1200 = 50x => x = 24%
This flexibility highlights the widespread applicability of these calculation methods.
Beyond Simple Calculations: Advanced Applications
Beyond basic percentage calculations, understanding this fundamental concept lays the groundwork for more complex applications:
-
Compound Interest: Calculating compound interest involves repeatedly applying percentage increases over time. Understanding basic percentage calculations is essential for comprehending this crucial financial concept.
-
Statistical Analysis: Percentages are used extensively in statistical analysis to represent proportions, frequencies, and probabilities. A solid grasp of percentage calculations is crucial for interpreting and drawing conclusions from statistical data.
-
Data Visualization: Percentages are commonly used in charts and graphs to visually represent proportions and trends within datasets. This is essential for effective communication of data insights.
-
Financial Modeling: Financial models often rely heavily on percentage calculations for forecasting, risk assessment, and scenario planning.
Conclusion: Mastering Percentage Calculations
Mastering the calculation of percentages, such as determining 6 as a percentage of 25, is a vital skill with numerous practical applications across various fields. By understanding the different methods – the fraction method, the decimal method, and the proportion method – you can confidently tackle diverse percentage problems and effectively interpret data in real-world situations. This skill not only empowers you to solve everyday problems but also equips you with a crucial foundation for more complex mathematical and financial analysis. The ability to quickly and accurately calculate percentages is an invaluable asset in both personal and professional contexts.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 5 And 25
May 24, 2025
-
5 Out Of 20 Is What Percent
May 24, 2025
-
2 3 Divided By 5 6 In Fraction Form
May 24, 2025
-
How Many More Hours Till 7 Am
May 24, 2025
-
How Many Hours Is 8pm To 8am
May 24, 2025
Related Post
Thank you for visiting our website which covers about 6 As A Percentage Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.