54 As A Product Of Prime Factors
listenit
Apr 01, 2025 · 5 min read
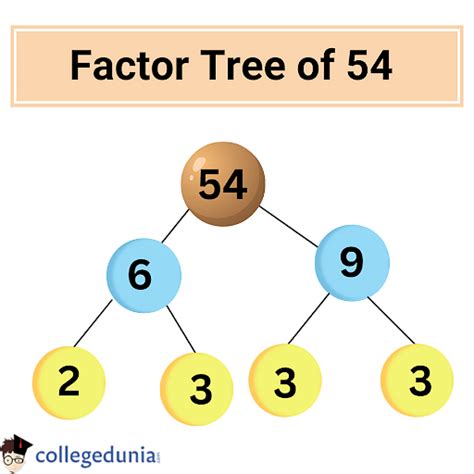
Table of Contents
54 as a Product of Prime Factors: A Deep Dive into Prime Factorization
Prime factorization, the process of breaking down a number into its prime number constituents, is a fundamental concept in number theory. Understanding this process unlocks deeper insights into the properties and behavior of numbers. This article delves into the prime factorization of 54, illustrating the method and exploring its applications. We will move beyond a simple answer and examine the broader context of prime factorization, its significance in mathematics, and practical uses.
Understanding Prime Numbers
Before embarking on the factorization of 54, let's revisit the definition of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. These numbers serve as the building blocks for all other natural numbers through prime factorization.
Key Characteristics of Prime Numbers:
- Divisibility: Prime numbers are only divisible by 1 and themselves.
- Infinitude: There are infinitely many prime numbers. This is a significant theorem in number theory, proving that the sequence of primes never ends.
- Uniqueness: The prime factorization of any composite number is unique (up to the order of the factors). This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 54
Now, let's proceed to find the prime factors of 54. There are several methods to achieve this, but a common approach involves successively dividing by prime numbers.
Method 1: Repeated Division
- Start with the smallest prime number, 2: 54 is an even number, so it's divisible by 2. 54 / 2 = 27.
- Move to the next prime number, 3: 27 is divisible by 3. 27 / 3 = 9.
- Continue with 3: 9 is also divisible by 3. 9 / 3 = 3.
- We've reached a prime number: The final result is 3.
Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3, or 2 x 3³.
Method 2: Factor Tree
A factor tree provides a visual representation of the factorization process.
54
/ \
2 27
/ \
3 9
/ \
3 3
This tree clearly shows the prime factors: 2, 3, 3, and 3. Again, this results in the prime factorization of 2 x 3³.
The Significance of Prime Factorization
The seemingly simple process of prime factorization holds significant importance across various mathematical domains:
- Number Theory: Prime factorization is fundamental to many theorems and concepts in number theory, including the study of modular arithmetic, cryptography, and the distribution of prime numbers.
- Cryptography: Many modern encryption methods rely heavily on the difficulty of factoring very large numbers into their prime factors. The security of RSA encryption, for example, depends on this computational challenge.
- Abstract Algebra: Prime factorization plays a crucial role in abstract algebra, particularly in ring theory and the study of ideal factorization.
- Simplifying Fractions: Prime factorization helps in simplifying fractions to their lowest terms by canceling common factors in the numerator and denominator. For instance, simplifying 54/72 involves finding the prime factorization of both numbers and then canceling common factors.
- Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization provides an efficient way to find the GCD and LCM of two or more numbers. The GCD is the largest number that divides all given numbers, while the LCM is the smallest number that is divisible by all given numbers.
Applications in Real-World Problems
While prime factorization might seem purely theoretical, it has practical applications:
- Inventory Management: Businesses use prime factorization to optimize inventory storage and distribution by identifying common factors in order quantities.
- Scheduling: Prime factorization can help in scheduling tasks, especially when dealing with recurring events with different cycles. Finding the LCM can determine when these events will coincide.
- Computer Science: Prime factorization is vital in computer algorithms and data structures, particularly in areas like hashing and data compression.
Beyond 54: Exploring Other Factorizations
Let's extend our understanding by examining the prime factorization of a few related numbers:
- 53: 53 is itself a prime number; its prime factorization is simply 53.
- 55: 55 = 5 x 11 (both 5 and 11 are prime numbers).
- 56: 56 = 2 x 2 x 2 x 7 = 2³ x 7.
- 57: 57 = 3 x 19.
Observing these examples, we notice the varied structures of prime factorizations. Some numbers are prime themselves, while others have multiple prime factors, potentially with repeated factors like in the case of 54 and 56.
Advanced Concepts Related to Prime Factorization
For those interested in delving deeper, some advanced concepts related to prime factorization include:
- The Fundamental Theorem of Arithmetic: This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, ignoring the order of the factors. This is a cornerstone of number theory.
- Sieve of Eratosthenes: This is an ancient algorithm for finding all prime numbers up to any given limit. It's an efficient method for generating a list of primes.
- Mersenne Primes: These are prime numbers that are one less than a power of two (2<sup>p</sup> - 1, where p is a prime number). Finding Mersenne primes is an ongoing area of research.
- The Riemann Hypothesis: This is one of the most important unsolved problems in mathematics. It relates to the distribution of prime numbers and has profound implications for number theory.
Conclusion: The Enduring Importance of Prime Factorization
Prime factorization, while seemingly simple in its application to a number like 54, represents a fundamental concept with far-reaching implications across numerous mathematical fields and practical applications. Its understanding unlocks the secrets of number structure and forms the basis for more complex mathematical theories and technologies. From simplifying fractions to securing online transactions, the power of prime factorization is undeniable. Whether you are a student of mathematics or a curious individual, grasping this concept is a significant step towards a deeper appreciation of the world of numbers.
Latest Posts
Latest Posts
-
How To Solve Multi Step Inequalities
Apr 02, 2025
-
Percent Composition Of Mg No3 2
Apr 02, 2025
-
How To Convert 3 8 Into A Decimal
Apr 02, 2025
-
Natural Resources Of The Northeast Region
Apr 02, 2025
-
How Many Unpaired Electrons Are In Sulfur
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 54 As A Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
