5 Is What Percent Of 23
listenit
May 24, 2025 · 4 min read
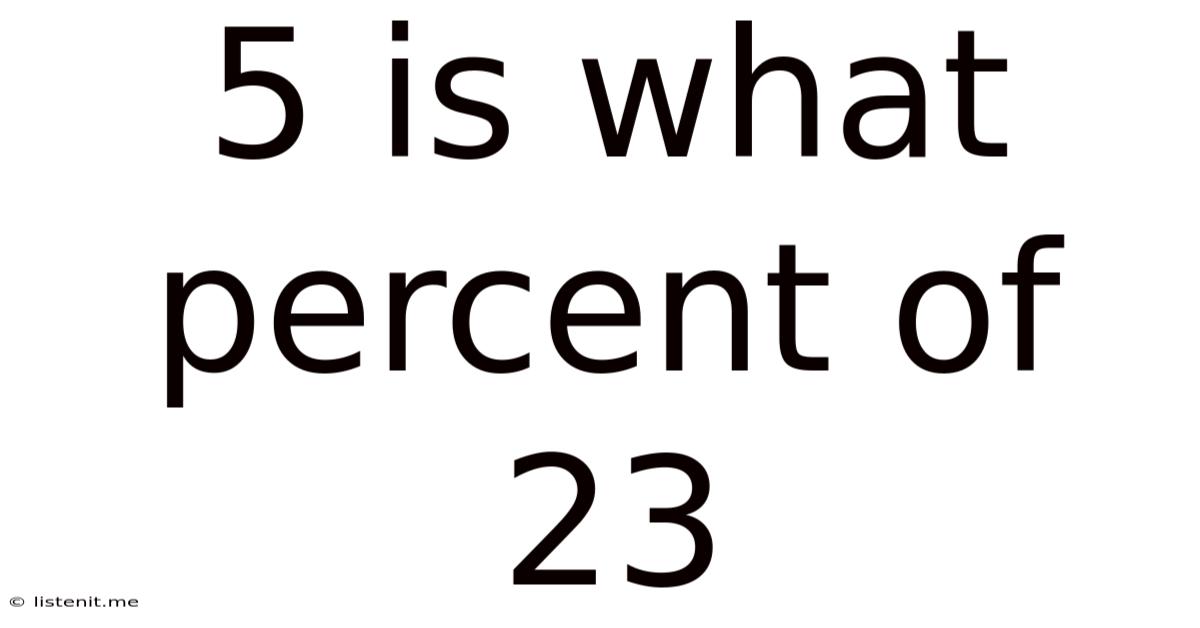
Table of Contents
5 is What Percent of 23? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific analysis and financial modeling. Understanding how to solve percentage problems is crucial for navigating the numerical world effectively. This article delves into the question, "5 is what percent of 23?", providing a detailed explanation of the calculation process, along with practical examples and tips for mastering percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin "per centum"). When we say "x percent," we mean x parts out of 100 equal parts. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Calculating "5 is What Percent of 23?"
To determine what percent 5 is of 23, we need to follow a simple formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 5
- Whole: 23
Therefore, the calculation is:
(5 / 23) * 100 = 21.739% (approximately)
Therefore, 5 is approximately 21.739% of 23.
Step-by-Step Breakdown
Let's break down the calculation into manageable steps:
-
Identify the Part and the Whole: Clearly define which number represents the "part" and which represents the "whole." In our problem, 5 is the part, and 23 is the whole.
-
Divide the Part by the Whole: Divide the "part" (5) by the "whole" (23). This gives us a decimal: 5 / 23 ≈ 0.21739
-
Multiply by 100: Multiply the decimal result by 100 to convert it into a percentage. 0.21739 * 100 ≈ 21.739
-
Express as a Percentage: Add the "%" symbol to indicate that the result is a percentage. The final answer is approximately 21.739%.
Rounding and Precision
The result, 21.739%, contains several decimal places. The level of precision required depends on the context. For many applications, rounding to one or two decimal places is sufficient (e.g., 21.74%). However, for situations demanding high accuracy, retaining more decimal places might be necessary. Always consider the context and specify the precision accordingly.
Practical Applications
Percentage calculations are ubiquitous in various real-world situations:
-
Sales and Discounts: Determining the discount amount on a sale item. For instance, a 20% discount on a $50 item means a savings of $10.
-
Taxes and Tips: Calculating sales tax or service tips. A 6% sales tax on a $100 purchase adds $6 to the total.
-
Financial Calculations: Calculating interest earned on savings accounts or interest paid on loans. Understanding compound interest requires a solid grasp of percentages.
-
Statistics and Data Analysis: Representing proportions and changes in data sets. Percentages are frequently used to summarize and interpret statistical findings.
-
Science and Engineering: Expressing concentrations, efficiencies, and other quantitative relationships.
Advanced Percentage Calculations
While the basic percentage formula is straightforward, more complex scenarios may arise:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 15% of a number is 30, the number is 200 (30 / 0.15 = 200).
-
Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, 25% of 80 is 20 (0.25 * 80 = 20).
-
Percentage Change: This involves calculating the percentage increase or decrease between two numbers. The formula is: [(New Value - Old Value) / Old Value] * 100.
-
Compound Interest: This is a more advanced calculation where interest earned is added to the principal, and subsequent interest is calculated on the increased amount.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to improve your understanding and speed is through consistent practice. Solve various percentage problems to build your confidence.
-
Use a Calculator: Utilize a calculator for complex calculations to avoid errors and save time. Many calculators have dedicated percentage functions.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles behind percentage calculations.
-
Break Down Complex Problems: If faced with a difficult problem, break it down into smaller, manageable steps.
-
Check Your Work: Always verify your answers to ensure accuracy.
Conclusion: Beyond the Calculation
This in-depth exploration of "5 is what percent of 23?" demonstrates that percentage calculations, while seemingly simple, are a foundation for numerous mathematical and real-world applications. By mastering the basic principles and applying the appropriate formulas, you'll be equipped to confidently tackle a wide range of percentage-related problems. Remember to practice consistently, leverage available tools, and ensure you deeply understand the underlying concepts. This will not only help you solve problems accurately but also foster a strong foundation for more advanced mathematical concepts. The ability to perform these calculations efficiently will undoubtedly enhance your skills in various areas, from personal finance to professional fields.
Latest Posts
Latest Posts
-
5 6 Divided By 1 3 In Fraction
May 25, 2025
-
25 To The Power Of 5
May 25, 2025
-
What Is 20 Percent Of 60 Dollars
May 25, 2025
-
Highest Common Factor Of 3 And 6
May 25, 2025
-
Write Quadratic Equation With Given Roots Calculator
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.