5/6 Divided By 1/3 In Fraction
listenit
May 25, 2025 · 5 min read
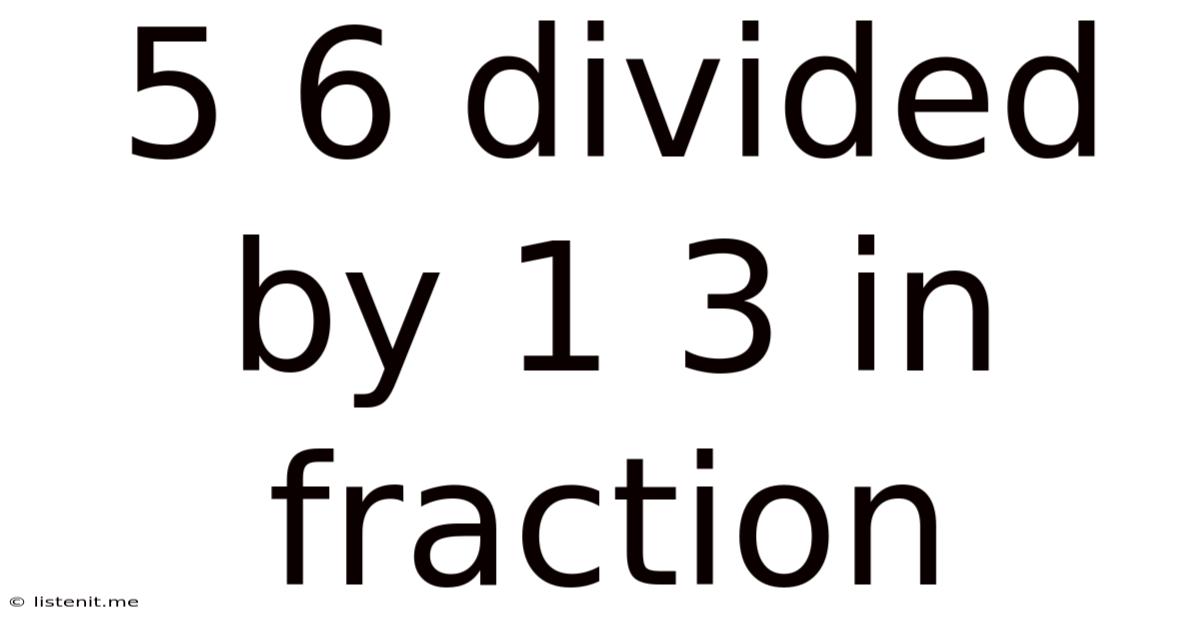
Table of Contents
5/6 Divided by 1/3: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through dividing 5/6 by 1/3, explaining the underlying principles and offering various approaches to solve this type of problem. We'll also explore the broader context of fraction division, providing you with the tools to tackle any similar problem confidently.
Understanding Fraction Division
Before diving into the specific calculation of 5/6 ÷ 1/3, let's solidify our understanding of fraction division. The core concept revolves around finding out "how many times" one fraction fits into another. For instance, 5/6 ÷ 1/3 asks: "How many times does 1/3 fit into 5/6?"
Unlike addition and subtraction, where we need common denominators, fraction division utilizes a different technique. The most common method involves inverting the second fraction (the divisor) and then multiplying. This is often summarized as "keep, change, flip."
- Keep: Keep the first fraction (the dividend) as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor), meaning reciprocal it.
Solving 5/6 Divided by 1/3
Now, let's apply this method to our problem: 5/6 ÷ 1/3
-
Keep: We keep the first fraction, 5/6, unchanged.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We flip the second fraction, 1/3, to its reciprocal, which is 3/1 or simply 3.
This transforms our division problem into a multiplication problem:
5/6 × 3
Now, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(5 × 3) / (6 × 1) = 15/6
Simplifying the Fraction
The result, 15/6, is an improper fraction (the numerator is larger than the denominator). We can simplify this by converting it to a mixed number or reducing it to its lowest terms.
To reduce the fraction, we find the greatest common divisor (GCD) of the numerator (15) and the denominator (6). The GCD of 15 and 6 is 3. We then divide both the numerator and the denominator by the GCD:
15 ÷ 3 / 6 ÷ 3 = 5/2
This simplified improper fraction, 5/2, can be further converted into a mixed number:
5 ÷ 2 = 2 with a remainder of 1. Therefore, 5/2 is equal to 2 1/2.
Alternative Approaches to Fraction Division
While the "keep, change, flip" method is widely used and efficient, there are alternative ways to approach fraction division. Understanding these alternative methods can provide a deeper understanding of the underlying principles.
Using Common Denominators
Though less commonly used for division, employing common denominators can be a helpful approach for those who find it more intuitive. This method involves converting both fractions to have the same denominator before performing the division.
Let's consider 5/6 ÷ 1/3 again. The least common denominator (LCD) of 6 and 3 is 6. We convert 1/3 to an equivalent fraction with a denominator of 6:
1/3 × 2/2 = 2/6
Now, we have:
5/6 ÷ 2/6
Since the denominators are the same, we can divide the numerators:
5 ÷ 2 = 5/2 or 2 1/2
Visual Representation
Visualizing fraction division can be especially helpful for beginners. Imagine you have a pizza cut into six slices (representing 5/6 of a pizza). You want to know how many 1/3 slices fit into the 5/6. You'd find that 2 and a half 1/3 slices fit into 5/6.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it finds practical applications in various real-world scenarios. Consider these examples:
-
Cooking and Baking: Recipes often require dividing ingredients. For example, if a recipe calls for 2/3 cup of flour and you want to halve the recipe, you'll need to divide 2/3 by 2 (or multiply by 1/2).
-
Sewing and Crafts: Cutting fabric or other materials often involves fraction division. If you need to divide a piece of fabric measuring 5/6 of a yard into thirds, you'll use fraction division.
-
Construction and Engineering: Precise measurements are crucial, and fraction division is employed extensively in calculating dimensions and materials.
-
Data Analysis: Working with datasets frequently involves proportions and ratios which often utilize fraction division.
Advanced Concepts Related to Fraction Division
Mastering basic fraction division opens doors to more advanced concepts:
-
Dividing Mixed Numbers: Problems involving mixed numbers require converting them into improper fractions before applying the division techniques discussed earlier. For example, dividing 2 1/2 by 1 1/3 would involve first converting them to 5/2 and 4/3 respectively.
-
Dividing Fractions with Variables: Algebra introduces fraction division involving variables. The principles remain the same, but algebraic manipulation is needed to simplify the expressions.
-
Complex Fractions: These fractions have fractions within the numerator or denominator (or both) and require careful application of fraction division rules to simplify.
Troubleshooting Common Mistakes in Fraction Division
Several common mistakes can arise when performing fraction division. Being aware of these potential pitfalls can help you avoid them:
-
Forgetting to flip the second fraction: This is the most common error. Remember the "keep, change, flip" rule.
-
Incorrect multiplication after flipping: Once you've flipped the second fraction, carefully multiply the numerators and denominators.
-
Failing to simplify the answer: Always reduce your final answer to its lowest terms or express it as a mixed number for clarity.
Conclusion: Mastering Fraction Division for Success
Fraction division, while initially appearing complex, is a fundamental skill with wide-ranging applications. By understanding the "keep, change, flip" method, exploring alternative approaches, and practicing regularly, you can confidently tackle any fraction division problem. This guide provides a solid foundation, enabling you to approach more complex scenarios with assurance and accuracy. Remember to practice consistently; the more you work with fractions, the more intuitive the process will become. Mastering fraction division is a significant step towards success in mathematics and its numerous real-world applications.
Latest Posts
Latest Posts
-
26 2 Miles In 3 Hours Pace
May 25, 2025
-
What Is The Percentage Of 10 Out Of 25
May 25, 2025
-
How To Calculate The Value Of A Pension
May 25, 2025
-
2 Root 2 Plus 2 Root 2
May 25, 2025
-
Greatest Common Divisor Of 45 And 30
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 1/3 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.