2 Root 2 Plus 2 Root 2
listenit
May 25, 2025 · 5 min read
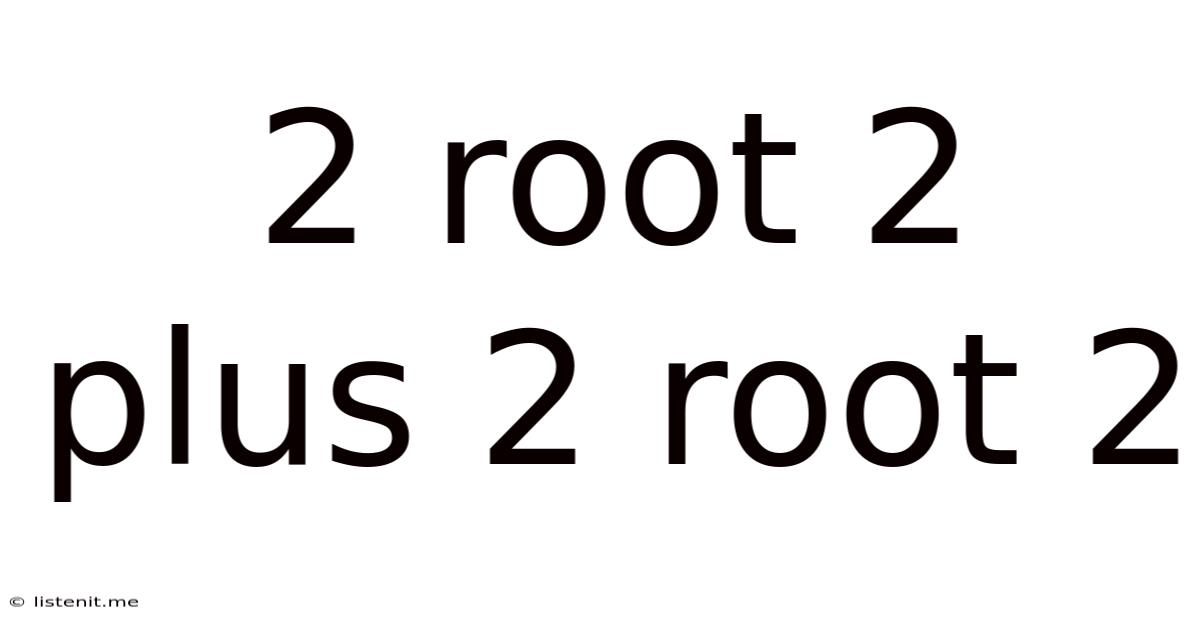
Table of Contents
Decoding the Mystery: 2√2 + 2√2 and its Implications
The seemingly simple mathematical expression, 2√2 + 2√2, often catches the eye of students and math enthusiasts alike. While its solution is straightforward, a deeper dive reveals interesting connections to fundamental mathematical concepts and applications in various fields. This article will explore this expression, unraveling its meaning, demonstrating its solution, and exploring its relevance in a broader mathematical context. We will delve into the properties of radicals, explore its geometrical interpretation, and touch upon its significance in algebra and beyond.
Understanding the Basics: Radicals and Square Roots
Before diving into the intricacies of 2√2 + 2√2, let's establish a strong foundation in understanding radicals, specifically square roots. A square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. The symbol '√' denotes the principal (non-negative) square root. For instance, √9 = 3 because 3 x 3 = 9. The number under the radical symbol (√) is called the radicand.
Key Properties of Radicals:
- √(a x b) = √a x √b: The square root of a product is the product of the square roots. This property is crucial when simplifying expressions involving radicals.
- √(a/b) = √a / √b: The square root of a quotient is the quotient of the square roots (provided 'b' is not zero).
- a√x + b√x = (a+b)√x: This is the crucial property that directly relates to our primary expression, 2√2 + 2√2. It highlights the fact that we can add or subtract radical terms that share the same radicand just like we add or subtract algebraic terms with the same variable.
Solving 2√2 + 2√2: A Step-by-Step Approach
Now, let's tackle the main expression: 2√2 + 2√2. Applying the property mentioned above, we can simplify this expression:
2√2 + 2√2 = (2 + 2)√2 = 4√2
Therefore, the simplified form of 2√2 + 2√2 is 4√2. This is a concise and exact representation of the expression.
Beyond Simplification: Geometric Interpretation and Real-World Applications
The result, 4√2, is not just a numerical value; it has a rich geometric interpretation. Consider a right-angled isosceles triangle with legs of length 2. Using the Pythagorean theorem (a² + b² = c²), the length of the hypotenuse (c) can be calculated:
c² = 2² + 2² = 8 c = √8 = √(4 x 2) = 2√2
Now, if we consider two such identical triangles placed side by side, the total length would be 2 x 2√2 = 4√2. This demonstrates the practical manifestation of our expression in geometric terms.
Real-world applications involving √2 and its multiples are abundant:
- Construction and Engineering: The √2 is fundamental in calculating diagonal measurements, particularly in structures built with square or rectangular components. Understanding this allows for precise measurements and material estimations.
- Computer Graphics and Game Development: √2 appears frequently in algorithms for calculating distances and rotations in two-dimensional and three-dimensional spaces. Accurate calculations are essential for realistic rendering and game physics.
- Physics and Engineering: The diagonal of a square is a frequent problem in many scenarios. When analyzing forces or velocities at angles, expressions similar to this are commonly encountered.
- Digital Signal Processing: Approximations and manipulation of irrational numbers like √2 are crucial in digital signal processing for various applications like audio and image processing.
Approximating the Value: Bridging Theory and Practice
While 4√2 is the exact value, it's often beneficial to approximate it to a decimal value for practical applications. The approximate value of √2 is 1.414. Therefore:
4√2 ≈ 4 x 1.414 = 5.656
This approximation is useful in scenarios where precise calculations are less critical than having a readily usable numerical representation.
Exploring Related Concepts: Irrational Numbers and Their Significance
The number √2 is a classic example of an irrational number – a number that cannot be expressed as a simple fraction (a ratio of two integers). This means its decimal representation continues infinitely without repeating. Understanding irrational numbers is crucial in advanced mathematical concepts like calculus and analysis.
The Significance of Irrational Numbers:
- Foundation of Calculus: Many fundamental concepts in calculus, such as limits and derivatives, rely heavily on the properties of irrational numbers.
- Geometry and Trigonometry: Irrational numbers like √2 and π (pi) are fundamental constants in geometric and trigonometric calculations.
- Number Theory: The study of irrational numbers is a significant area of research in number theory, a branch of mathematics focused on the properties of numbers.
Extending the Concept: Generalizing the Expression
We can generalize the expression 2√2 + 2√2 to encompass similar scenarios with different coefficients and radicands:
a√x + b√x = (a + b)√x
This generalized form underscores the fundamental algebraic principle of combining like terms, applicable to various mathematical expressions beyond just radicals.
Conclusion: The Beauty of Simplicity and its Profound Implications
The seemingly trivial expression 2√2 + 2√2, upon closer inspection, opens up a fascinating world of mathematical concepts and their applications in various fields. From its simple solution to its geometric interpretation and its connection to irrational numbers, this expression showcases the beauty of mathematical simplicity and its profound implications in the real world. Understanding this expression, and the underlying mathematical principles, provides a strong foundation for further exploration of more complex mathematical concepts and their practical applications. The elegance and utility of mathematics are beautifully illustrated by this deceptively simple expression, reminding us of the interconnectedness and power of mathematical ideas.
Latest Posts
Latest Posts
-
14v 6 2 5 7v 4
May 25, 2025
-
What Is The Greatest Common Factor Of 48 And 30
May 25, 2025
-
What Is The Gcf Of 56 And 35
May 25, 2025
-
Find The Probability Of Z Occurring In The Indicated Region
May 25, 2025
-
22 Out Of 40 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about 2 Root 2 Plus 2 Root 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.