4x Y 1 In Slope Intercept Form
listenit
May 10, 2025 · 6 min read
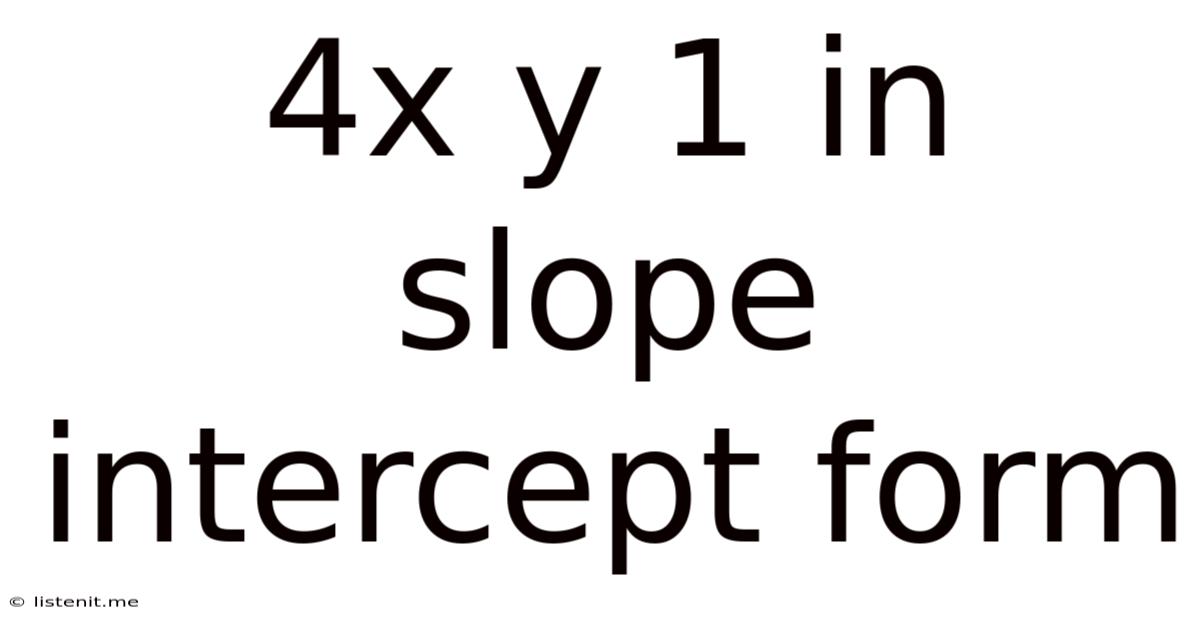
Table of Contents
Understanding and Applying the Slope-Intercept Form: A Deep Dive into 4x + y = 1
The equation 4x + y = 1 represents a linear relationship between two variables, x and y. While useful in its current form, converting it to the slope-intercept form (y = mx + b) offers significant advantages in understanding and visualizing the line's characteristics. This form clearly reveals the slope (m) and the y-intercept (b), providing crucial information for graphing, analyzing, and making predictions based on the linear relationship. This article will delve into the process of converting 4x + y = 1 into slope-intercept form, explain the significance of the slope and y-intercept, and explore various applications of this form.
Converting 4x + y = 1 to Slope-Intercept Form
The slope-intercept form, y = mx + b, expresses a linear equation where 'm' represents the slope and 'b' represents the y-intercept. To convert 4x + y = 1 into this form, we need to isolate 'y' on one side of the equation:
- Subtract 4x from both sides: This step removes the '4x' term from the left side, leaving 'y' isolated. The equation becomes: y = -4x + 1
Now, the equation is in the slope-intercept form (y = mx + b):
-
m = -4: This is the slope of the line. It indicates that for every one-unit increase in x, y decreases by four units. The negative slope signifies a downward trend.
-
b = 1: This is the y-intercept. It represents the point where the line intersects the y-axis (where x = 0). In this case, the line crosses the y-axis at the point (0, 1).
Understanding the Slope (m = -4)
The slope, -4, is a crucial characteristic of the line. It quantifies the steepness and direction of the line. A negative slope indicates a downward trend from left to right. Let's explore this further:
-
Steepness: The absolute value of the slope (|-4| = 4) indicates the steepness. A slope of 4 is relatively steep, implying a significant change in y for a small change in x.
-
Rate of Change: The slope represents the rate of change of y with respect to x. For every one-unit increase in x, y decreases by four units. This constant rate of change is a defining feature of linear relationships.
-
Parallel Lines: Any other line with a slope of -4 will be parallel to the line represented by y = -4x + 1. Parallel lines never intersect.
Understanding the Y-Intercept (b = 1)
The y-intercept, 1, is the point where the line crosses the y-axis. This is the value of y when x is zero. It provides a crucial point for graphing the line:
-
Starting Point: The y-intercept serves as a convenient starting point when graphing the line. By plotting the point (0, 1), we have one point on the line.
-
Intersection with Y-axis: The y-intercept is the only point on the line that lies directly on the y-axis.
-
Significance in Applications: In real-world applications, the y-intercept might represent an initial value, a starting point, or a base value. For instance, if this equation models a cost function, the y-intercept might represent a fixed cost regardless of the number of units produced.
Graphing the Line y = -4x + 1
Now that we have the slope (-4) and the y-intercept (1), we can easily graph the line:
-
Plot the y-intercept: Mark the point (0, 1) on the y-axis.
-
Use the slope to find another point: The slope is -4, which can be expressed as -4/1. This means for every 1 unit increase in x, y decreases by 4 units. Starting from (0, 1), move 1 unit to the right and 4 units down. This brings us to the point (1, -3).
-
Draw the line: Draw a straight line through the points (0, 1) and (1, -3). This line represents the equation y = -4x + 1.
Applications of the Slope-Intercept Form
The slope-intercept form is incredibly versatile and finds applications in various fields:
1. Economics and Finance:
-
Cost Functions: Linear equations in slope-intercept form are frequently used to model cost functions. The y-intercept represents fixed costs, while the slope represents the variable cost per unit.
-
Demand and Supply Curves: Supply and demand curves in economics are often represented by linear equations. The slope indicates the responsiveness of quantity demanded or supplied to changes in price.
2. Physics:
-
Motion: Equations of motion, particularly those involving constant acceleration, can be expressed in slope-intercept form. The slope represents velocity, and the y-intercept might represent the initial position.
-
Fluid Dynamics: Linear relationships between pressure and flow rate in fluid systems are often modeled using slope-intercept form.
3. Engineering:
-
Stress-Strain Relationships: In material science, the relationship between stress and strain for certain materials can be approximated by a linear equation, which can be expressed in slope-intercept form. The slope represents the Young's modulus of the material.
-
Electrical Circuits: Ohm's Law (V = IR), which describes the relationship between voltage (V), current (I), and resistance (R), can be represented in slope-intercept form if resistance is constant.
4. Computer Science:
-
Linear Regression: In machine learning and statistics, linear regression aims to find the best-fitting line through a set of data points. The resulting equation is typically expressed in slope-intercept form.
-
Algorithm Analysis: The time or space complexity of certain algorithms can be described using linear equations in slope-intercept form.
5. Everyday Life:
-
Calculating Distances: If you're traveling at a constant speed, you can use a linear equation in slope-intercept form to calculate the distance traveled based on time.
-
Pricing Models: Many pricing models in retail, especially those with a fixed fee and a per-unit charge, can be represented using slope-intercept form.
Advanced Applications and Considerations
While the basic applications above highlight the versatility of the slope-intercept form, its use extends to more complex scenarios:
-
Systems of Equations: Solving systems of linear equations often involves manipulating equations into slope-intercept form to identify points of intersection or determine if the lines are parallel.
-
Inequalities: The slope-intercept form can be easily adapted to represent linear inequalities, which are useful for modeling constraints or limitations in optimization problems.
-
Multivariable Calculus: Though the basic form deals with two variables, the concepts of slope (gradient) and intercept extend to higher dimensions in multivariable calculus.
Conclusion
Converting the equation 4x + y = 1 into slope-intercept form (y = -4x + 1) unlocks a wealth of information about the line it represents. Understanding the slope and y-intercept allows for easy graphing, analysis, and application in various fields. From simple calculations to complex mathematical models, the slope-intercept form remains a powerful tool for understanding and representing linear relationships. Its versatility makes it an essential concept in mathematics, science, and various professional fields. Mastering the slope-intercept form provides a strong foundation for further exploration of linear algebra and other mathematical concepts. The ability to easily visualize and interpret linear relationships is crucial for problem-solving and decision-making in countless applications.
Latest Posts
Latest Posts
-
Graph X 1 On A Number Line
May 10, 2025
-
Noble Gases Do Not Receive Electronegativity Values Because
May 10, 2025
-
Which Is The Graph Of 2x 4y 6
May 10, 2025
-
Organelle That Is The Site Of Protein Synthesis
May 10, 2025
-
Simplify Ln E Ln E2x Ln 1
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4x Y 1 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.