Simplify Ln E Ln E2x Ln 1
listenit
May 10, 2025 · 4 min read
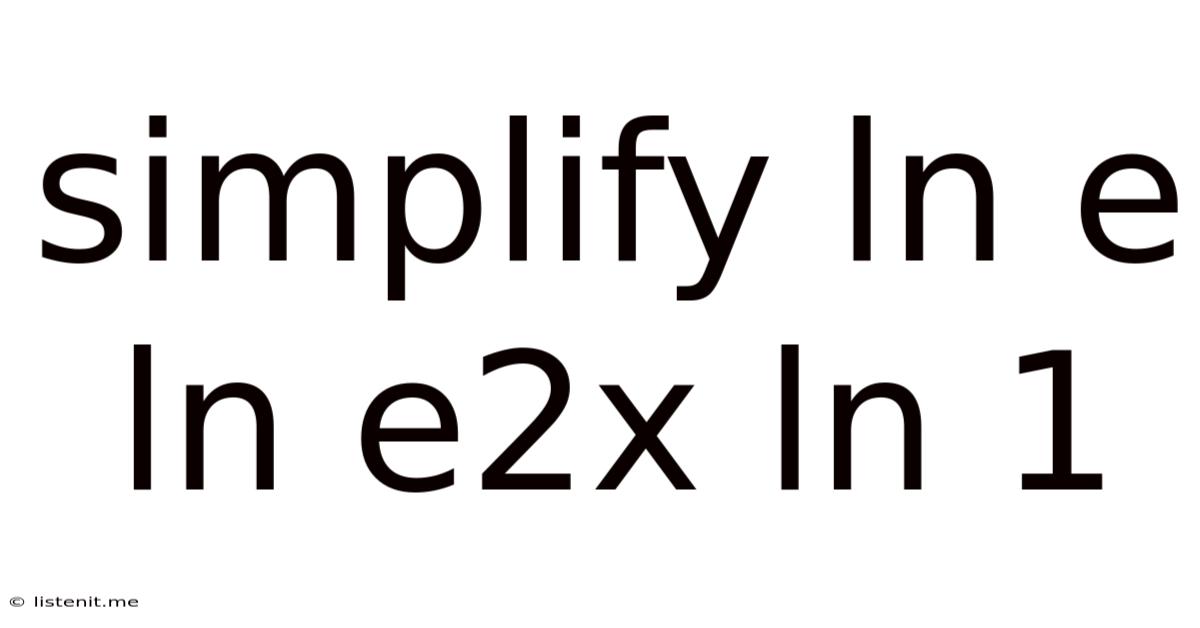
Table of Contents
Simplifying Logarithmic Expressions: ln e, ln e^(2x), and ln 1
Understanding logarithmic functions is crucial for success in mathematics, particularly calculus and its applications. This article delves into the simplification of three specific logarithmic expressions: ln e, ln e^(2x), and ln 1. We'll explore the underlying principles, provide step-by-step solutions, and offer practical examples to solidify your understanding. We will also touch upon the broader context of logarithmic simplification and its relevance in various mathematical fields.
Understanding Natural Logarithms (ln)
Before we tackle the simplification, let's establish a strong foundation in natural logarithms. The natural logarithm, denoted as ln x or logₑ x, is a logarithm with base e, where e is Euler's number, an irrational mathematical constant approximately equal to 2.71828. The natural logarithm is the inverse function of the exponential function e<sup>x</sup>. This inverse relationship is fundamental to simplifying logarithmic expressions. It means that:
- ln(e<sup>x</sup>) = x for all x
- e<sup>ln(x)</sup> = x for x > 0
These properties are the keys to unlocking the simplifications we're aiming for.
Simplifying ln e
This is the simplest of the three expressions. Recall that the natural logarithm, ln, has a base of e. Therefore, ln e is asking: "To what power must e be raised to equal e?" The answer is clearly 1.
Therefore:
ln e = 1
Simplifying ln e^(2x)
This expression involves a natural logarithm of an exponential function with base e. Here, we leverage the property that ln(e<sup>x</sup>) = x. In this case, x = 2x.
Step-by-step simplification:
- Identify the exponential function: We have e^(2x) inside the logarithm.
- Apply the inverse property: Using the property ln(e<sup>x</sup>) = x, we substitute 2x for x.
- Simplification: This directly gives us the simplified answer.
Therefore:
ln e^(2x) = 2x
Simplifying ln 1
This expression involves the natural logarithm of 1. To simplify this, we consider the definition of a logarithm. The question "ln 1 = ?" is equivalent to asking: "To what power must e be raised to equal 1?" Any non-zero number raised to the power of 0 equals 1. Therefore:
ln 1 = 0
Practical Applications and Examples
These simplifications aren't just theoretical exercises; they have wide-ranging applications in various mathematical fields, especially in calculus and its applications in physics, engineering, and finance. Let's explore some illustrative examples:
Example 1: Derivative of a Logarithmic Function
Let's consider finding the derivative of the function f(x) = ln(e^(3x²)).
- Simplify the expression: First, using the property ln(e<sup>x</sup>) = x, we simplify ln(e^(3x²)) to 3x².
- Differentiate: Now, we differentiate the simplified function f(x) = 3x² with respect to x: f'(x) = 6x.
This illustrates how simplifying logarithmic expressions using the properties we've discussed significantly simplifies the process of differentiation.
Example 2: Solving Logarithmic Equations
Suppose we have the equation ln(x) = 2. To solve for x, we use the definition of the natural logarithm and the exponential function:
- Rewrite in exponential form: The equation ln(x) = 2 can be rewritten as e² = x.
- Calculate the value: Using a calculator or mathematical software, we find that e² ≈ 7.389. Therefore, x ≈ 7.389.
Example 3: Financial Modeling
In financial modeling, the natural logarithm is frequently used to model growth rates. For instance, the continuous compounding interest formula is: A = Pe^(rt), where A is the future value, P is the principal, r is the interest rate, and t is the time. The natural logarithm can be used to solve for any of these variables, provided the others are known.
Beyond the Basics: More Complex Logarithmic Simplifications
While we've focused on relatively straightforward expressions, the principles discussed extend to more complex scenarios. For instance, consider simplifying an expression like: ln(e^(3x) * e^(2y)). Here, we can use the properties of logarithms:
- ln(ab) = ln(a) + ln(b)
- ln(a/b) = ln(a) - ln(b)
Applying these properties, we can simplify the expression as follows:
ln(e^(3x) * e^(2y)) = ln(e^(3x)) + ln(e^(2y)) = 3x + 2y.
Conclusion: Mastering Logarithmic Simplification
Simplifying logarithmic expressions, particularly those involving the natural logarithm, is a foundational skill in mathematics and its various applications. Understanding the inverse relationship between the natural logarithm and the exponential function, along with the properties of logarithms, is crucial for efficient simplification. Through practice and applying the techniques outlined in this article, you can master this essential skill, improving your problem-solving capabilities in mathematics, calculus, and beyond. The examples provided demonstrate the practical implications of logarithmic simplification, highlighting its importance across diverse mathematical and applied contexts. Remember to continually practice these techniques to enhance your understanding and proficiency.
Latest Posts
Latest Posts
-
Writing An Inequality In Interval Notation
May 10, 2025
-
How To Find Instantaneous Velocity On A Position Time Graph
May 10, 2025
-
Which Is The Most Stable Carbocation
May 10, 2025
-
12 Is 150 Percent Of What Number
May 10, 2025
-
What Part Of Speech Is Year
May 10, 2025
Related Post
Thank you for visiting our website which covers about Simplify Ln E Ln E2x Ln 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.