Which Is The Graph Of 2x 4y 6
listenit
May 10, 2025 · 5 min read
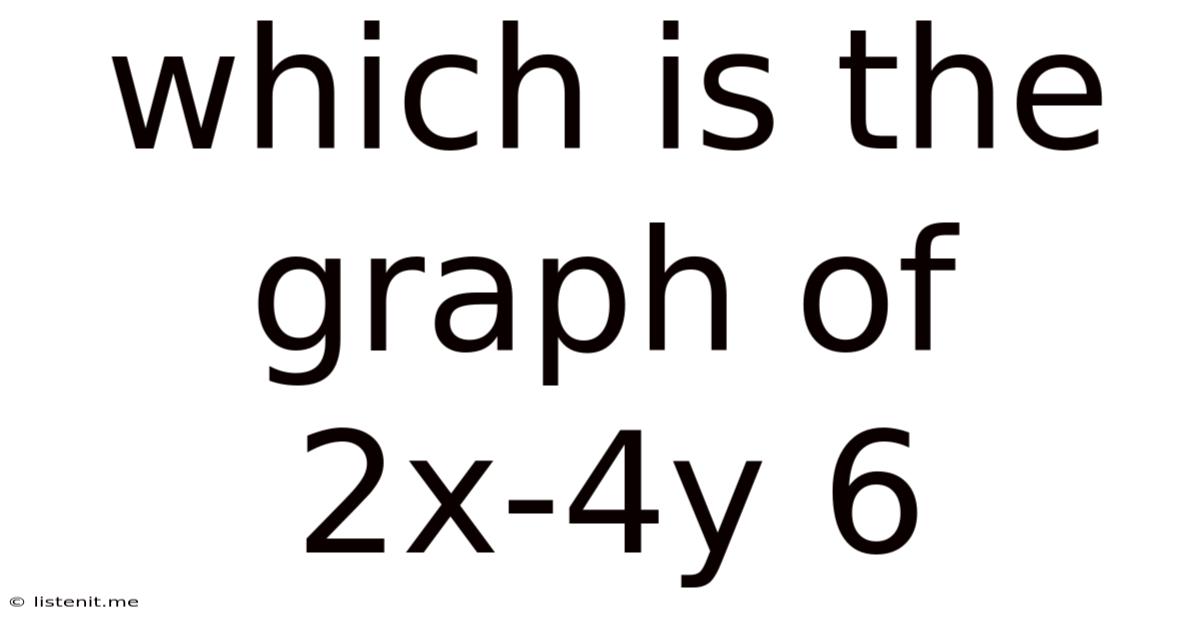
Table of Contents
Which is the Graph of 2x + 4y = 6? A Comprehensive Guide to Linear Equations and Their Visual Representations
Understanding linear equations and their graphical representations is fundamental to algebra and numerous applications in science, engineering, and finance. This article delves deep into the equation 2x + 4y = 6, exploring its characteristics, how to graph it, and the broader context of linear equations in general. We'll cover various methods for graphing, interpreting the slope and intercepts, and address common misconceptions.
Understanding the Equation: 2x + 4y = 6
The equation 2x + 4y = 6 is a linear equation in two variables, x and y. A linear equation represents a straight line when graphed on a Cartesian coordinate system. The equation is written in the standard form, Ax + By = C, where A, B, and C are constants. In our case, A = 2, B = 4, and C = 6.
Key Characteristics of the Equation
- Linearity: The highest power of both x and y is 1. This is the defining characteristic of a linear equation.
- Standard Form: The equation is presented in the standard form, which is useful for certain calculations and manipulations.
- Multiple Representations: The same line can be represented in different forms, such as slope-intercept form (y = mx + b) and point-slope form. We will explore these alternative representations later in the article.
Methods for Graphing 2x + 4y = 6
There are several ways to graph the linear equation 2x + 4y = 6. Let's explore the most common methods:
1. The Intercept Method
This method utilizes the x-intercept and the y-intercept to plot the line.
-
X-intercept: To find the x-intercept, set y = 0 and solve for x. 2x + 4(0) = 6 2x = 6 x = 3 The x-intercept is (3, 0).
-
Y-intercept: To find the y-intercept, set x = 0 and solve for y. 2(0) + 4y = 6 4y = 6 y = 6/4 = 3/2 = 1.5 The y-intercept is (0, 1.5).
Plot these two points (3, 0) and (0, 1.5) on the Cartesian coordinate system and draw a straight line passing through them. This line represents the graph of 2x + 4y = 6.
2. The Slope-Intercept Method
This method uses the slope (m) and the y-intercept (b) to graph the line. The slope-intercept form of a linear equation is y = mx + b.
First, we need to rewrite the equation 2x + 4y = 6 in slope-intercept form:
4y = -2x + 6 y = (-2/4)x + 6/4 y = (-1/2)x + 3/2
Now, we can identify the slope and y-intercept:
- Slope (m): m = -1/2. This indicates that for every 2 units increase in x, y decreases by 1 unit. The negative slope signifies a downward-sloping line.
- Y-intercept (b): b = 3/2 = 1.5. This is the point where the line intersects the y-axis.
Plot the y-intercept (0, 1.5). Then, using the slope, move 2 units to the right and 1 unit down to find another point on the line. Repeat this process to plot more points if needed. Draw a straight line through all the points.
3. Using Two Points
This method involves finding any two points that satisfy the equation and plotting them to draw the line. We can choose arbitrary values for x and solve for the corresponding y values (or vice-versa).
For example:
- If x = 1: 2(1) + 4y = 6 => 4y = 4 => y = 1. Point (1,1)
- If x = -1: 2(-1) + 4y = 6 => 4y = 8 => y = 2. Point (-1, 2)
Plot these two points (1,1) and (-1, 2) and draw a straight line passing through them.
Interpreting the Graph
The graph of 2x + 4y = 6 is a straight line with a negative slope, intersecting the x-axis at (3,0) and the y-axis at (0, 1.5). The slope of -1/2 indicates the rate of change of y with respect to x. Each point on the line represents a solution to the equation 2x + 4y = 6.
Applications of Linear Equations
Linear equations have vast applications across many fields:
- Physics: Describing motion, relationships between forces and accelerations.
- Engineering: Modeling electrical circuits, structural analysis.
- Economics: Supply and demand curves, linear programming.
- Finance: Calculating interest, projecting investments.
- Computer Science: Representing relationships between variables, in algorithms and data structures.
Addressing Common Misconceptions
- Non-linear equations: It's crucial to remember that only equations where the highest power of the variables is 1 represent straight lines. Higher powers result in curves.
- Slope and Intercept: Understanding the meaning of slope and y-intercept is vital for interpreting the graph and its real-world implications.
- Multiple representations: The same line can be represented in different forms (standard, slope-intercept, point-slope). Knowing how to convert between these forms is important.
Conclusion
Graphing linear equations, such as 2x + 4y = 6, is a fundamental skill in mathematics. Understanding the different methods for graphing, interpreting the slope and intercepts, and appreciating the broad applications of linear equations is essential for success in many academic and professional fields. This comprehensive guide aims to equip you with the knowledge and techniques to confidently approach and solve such problems. By practicing the methods outlined above, you'll build a strong foundation in linear algebra and its practical applications. Remember to always check your work and ensure your graph accurately reflects the equation. Further exploration into more complex equations and their graphical representations will solidify your understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
What Is The Lcm Of 12 16
May 10, 2025
-
List The Following Ions In Order Of Increasing Ionic Radius
May 10, 2025
-
729 To The Power Of 1 3
May 10, 2025
-
Copper Has Two Naturally Occurring Isotopes
May 10, 2025
-
1 And 1 6 As A Decimal
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Graph Of 2x 4y 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.