4 Out Of 22 As A Percentage
listenit
May 25, 2025 · 5 min read
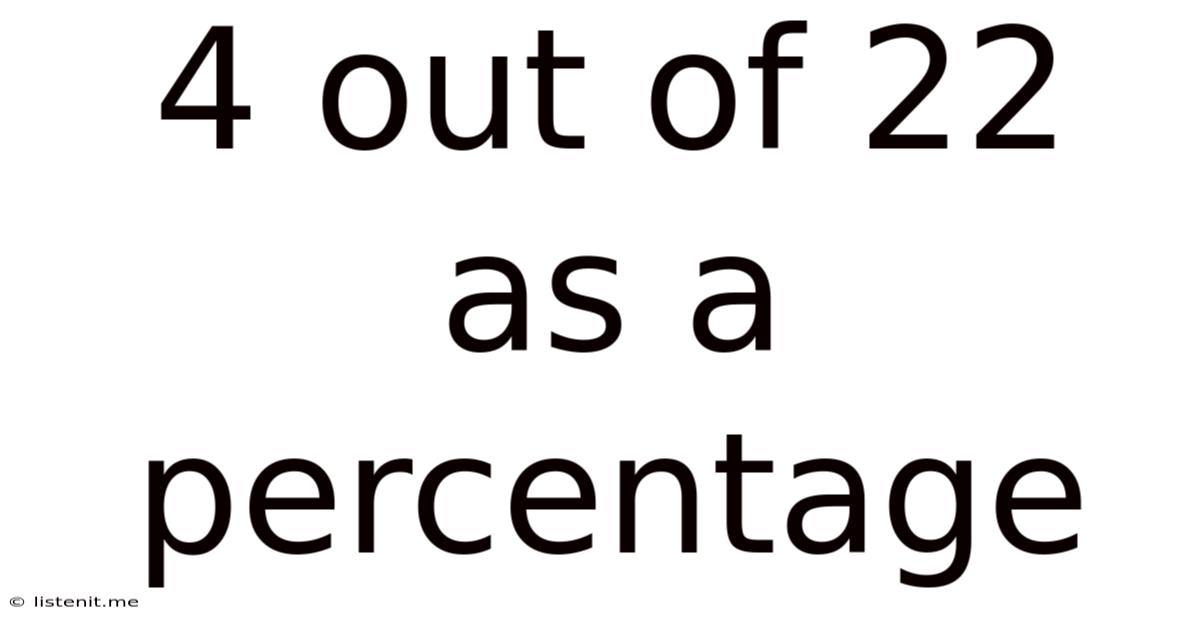
Table of Contents
4 Out of 22 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into how to calculate "4 out of 22 as a percentage," providing a detailed explanation of the process and exploring various applications of percentage calculations. We'll also cover different methods, address potential misconceptions, and offer practical examples to solidify your understanding.
Understanding the Basics of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentage is %. For instance, 50% means 50 out of 100, which can also be expressed as the fraction 50/100 or the decimal 0.5.
Calculating 4 out of 22 as a Percentage: The Step-by-Step Approach
To determine what percentage 4 out of 22 represents, we'll follow these simple steps:
Step 1: Express the values as a fraction.
The problem "4 out of 22" can be written as the fraction 4/22.
Step 2: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
4 ÷ 22 ≈ 0.1818
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.1818 × 100 ≈ 18.18%
Therefore, 4 out of 22 is approximately 18.18%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are alternative approaches you can use, depending on your preference and the tools available.
Method 1: Using Proportions
You can set up a proportion to solve this:
4/22 = x/100
Cross-multiply:
22x = 400
Solve for x:
x = 400/22 ≈ 18.18
Therefore, x ≈ 18.18%, confirming our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 4 ÷ 22 and then multiply by 100 to obtain the percentage. This method provides a quick and efficient way to calculate percentages.
Method 3: Simplifying the Fraction First
Before converting to a decimal, you can simplify the fraction 4/22 by dividing both the numerator and denominator by their greatest common divisor, which is 2:
4/22 = 2/11
Now, convert the simplified fraction 2/11 to a decimal:
2 ÷ 11 ≈ 0.1818
Then convert the decimal to a percentage:
0.1818 × 100 ≈ 18.18%
This method can sometimes make the calculation easier, particularly with larger numbers.
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous real-world applications:
1. Financial Calculations:
- Discounts: Calculating discounts on products is a common application. For example, a 20% discount on a $100 item would be $20 (100 x 0.20).
- Taxes: Determining the amount of sales tax or income tax payable involves percentage calculations.
- Interest Rates: Calculating simple or compound interest on loans or investments requires understanding percentages.
- Investment Returns: Analyzing investment performance often involves calculating percentage returns or losses.
2. Data Analysis and Statistics:
- Proportions and Ratios: Percentages are frequently used to express proportions and ratios in data analysis. For example, representing the percentage of males versus females in a population.
- Probability: Percentages are used to express probabilities, such as the likelihood of a certain event occurring.
- Surveys and Polls: Survey results are often presented as percentages to show the proportion of respondents who chose a particular option.
3. Everyday Life:
- Tip Calculation: Calculating a tip in a restaurant usually involves determining a percentage of the bill.
- Grade Calculation: Many grading systems utilize percentages to represent student performance.
- Cooking and Baking: Recipes sometimes specify ingredients as percentages of the total weight or volume.
Addressing Common Misconceptions about Percentages
Several common misconceptions surrounding percentages can lead to errors in calculations.
Misconception 1: Adding Percentages Directly
You cannot simply add percentages directly unless they are based on the same whole. For instance, a 10% increase followed by a 10% decrease does not result in a net change of 0%.
Misconception 2: Confusing Percentage Change with Absolute Change
A percentage change refers to the relative change compared to the initial value, while an absolute change represents the actual difference between two values. These are not interchangeable.
Misconception 3: Incorrectly Interpreting Percentage Points
A percentage point refers to the absolute difference between two percentages, not the percentage difference. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Advanced Percentage Calculations
Beyond simple calculations like "4 out of 22 as a percentage," understanding more complex percentage scenarios is crucial:
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two values involves finding the difference between them, dividing it by the original value, and multiplying by 100.
-
Percentage of a Percentage: Finding a percentage of a percentage requires multiplying the two percentages together. For example, finding 20% of 50% involves calculating 0.20 x 0.50 = 0.10, or 10%.
-
Successive Percentage Changes: Calculating the effect of multiple successive percentage changes can be more involved and requires careful consideration of the order of operations.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is an essential skill for navigating various aspects of life, from managing personal finances to analyzing data and making informed decisions. By understanding the fundamental concepts, different calculation methods, and potential pitfalls, you can confidently tackle percentage problems of varying complexity. Remember to always double-check your work and consider using different methods to verify your results. The ability to accurately calculate and interpret percentages is a valuable asset in both personal and professional settings. This guide provides a solid foundation for building your proficiency in this crucial mathematical skill.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 147
May 25, 2025
-
What Is 1 Hour From Now
May 25, 2025
-
What Is 20 Of 70 Dollars
May 25, 2025
-
1 2 Divided By 1 6
May 25, 2025
-
Lcm Of 3 7 And 10
May 25, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 22 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.