Lcm Of 3 7 And 10
listenit
May 25, 2025 · 4 min read
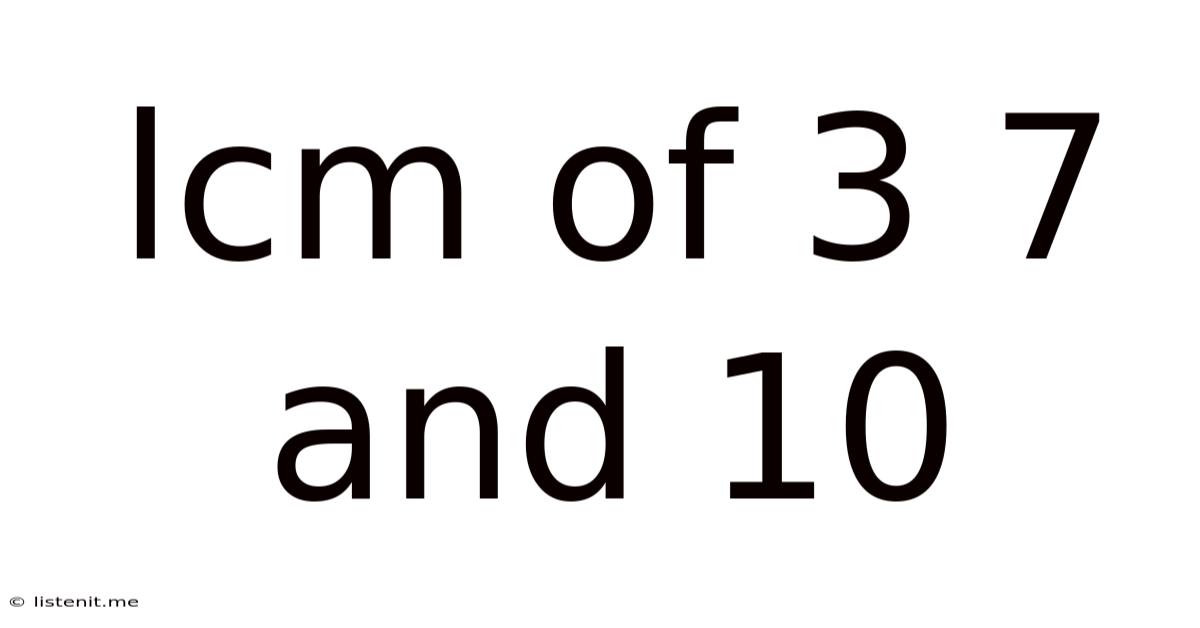
Table of Contents
Finding the LCM of 3, 7, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will delve deep into the process of calculating the LCM of 3, 7, and 10, exploring different methods and their underlying principles. We'll also touch upon the broader significance of LCMs and their practical use.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3, 7, and 10, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Distinguishing LCM from GCD
It's crucial to differentiate the LCM from the greatest common divisor (GCD). The GCD is the largest positive integer that divides all the given integers without leaving a remainder. While seemingly opposites, the LCM and GCD are related through a fundamental mathematical relationship, which we'll explore later.
Methods for Calculating the LCM of 3, 7, and 10
Several methods can be employed to determine the LCM of 3, 7, and 10. Let's examine the most common approaches:
1. Listing Multiples Method
This is a straightforward, intuitive method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By inspecting the lists, we can see that the smallest multiple common to 3, 7, and 10 is 210.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 3: 3¹
- Prime factorization of 7: 7¹
- Prime factorization of 10: 2¹ × 5¹
To find the LCM, we take the highest power of each prime factor present in the factorizations: 2¹, 3¹, 5¹, and 7¹. Multiplying these together, we get: 2 × 3 × 5 × 7 = 210.
3. Using the Formula: LCM(a, b, c) = (a × b × c) / GCD(a, b, c)
This method leverages the relationship between the LCM and the GCD. However, this formula is only directly applicable to two numbers. To use it for three numbers, we need to apply it iteratively. First find the LCM of two of the numbers and then find the LCM of the result and the third number.
First, let's find the LCM of 3 and 7. Since 3 and 7 are both prime numbers, their GCD is 1. Thus, their LCM is 3 x 7 = 21.
Next, we find the LCM of 21 and 10. The prime factorization of 21 is 3 x 7 and the prime factorization of 10 is 2 x 5. The LCM(21, 10) is 2 x 3 x 5 x 7 = 210.
Therefore, the LCM of 3, 7, and 10 is 210.
Applications of LCM
The concept of LCM finds practical applications in various areas:
1. Scheduling and Synchronization
Imagine you have three machines that operate on cycles of 3, 7, and 10 hours respectively. To determine when all three machines will complete a cycle simultaneously, you need to find the LCM of these numbers. The LCM, 210, indicates that all three machines will complete a cycle at the same time after 210 hours.
2. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the common denominator, simplifying the process of adding or subtracting the fractions.
3. Number Theory and Cryptography
LCMs play a vital role in number theory and its applications, such as in cryptography, where modular arithmetic and the properties of LCM are fundamental to developing secure encryption methods.
4. Real-World Scenarios
From calculating the time it takes for events to occur simultaneously to determining the frequency of shared events, the LCM is an integral tool for resolving various real-world problems.
Conclusion: Mastering LCM Calculations
Finding the LCM of 3, 7, and 10, as demonstrated, can be achieved through several methods. The choice of method often depends on the complexity of the numbers involved. The prime factorization method is generally considered the most efficient and insightful for larger numbers, while the listing method is suitable for smaller sets. Understanding these methods, along with the practical applications of LCMs, provides a solid foundation for tackling more complex mathematical problems and real-world scenarios. Remember that consistent practice is key to mastering these techniques and applying them effectively. The ability to efficiently calculate LCMs is a valuable skill with broad applicability in mathematics and beyond.
Latest Posts
Latest Posts
-
2000 Days Is How Many Years
May 25, 2025
-
What Is The Greatest Common Factor Of 12 And 27
May 25, 2025
-
How Long Ago Was 12 Weeks
May 25, 2025
-
The Equation Below Shows The Formula For Calculating
May 25, 2025
-
11k A Month Is How Much A Year
May 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 7 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.