4 Is What Percent Of 19
listenit
May 25, 2025 · 5 min read
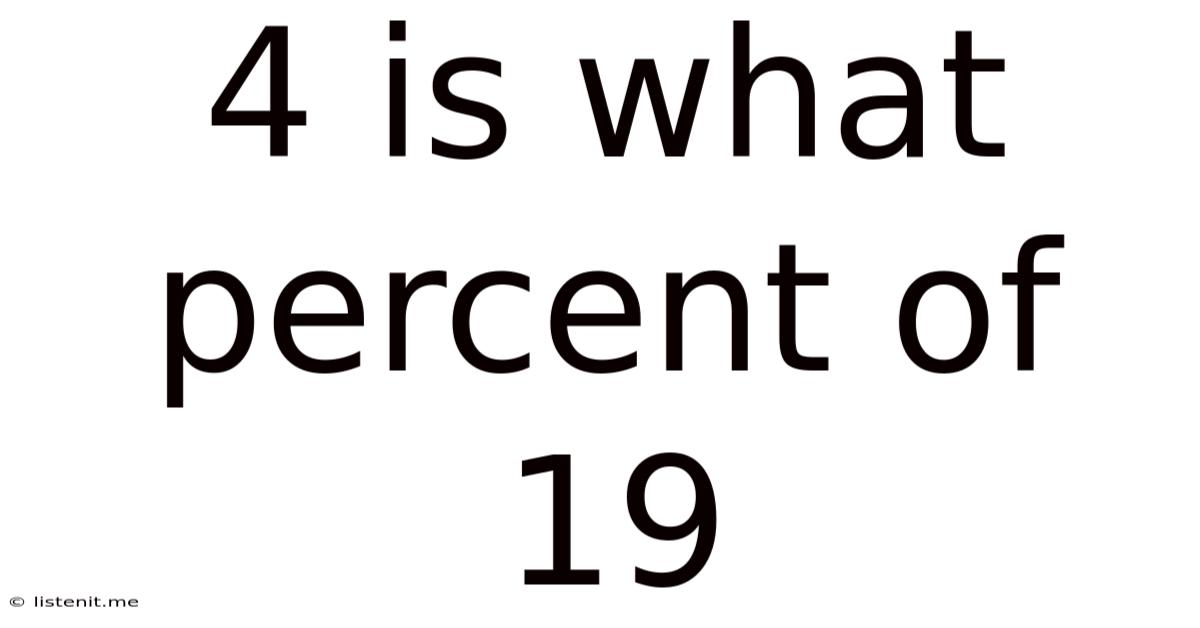
Table of Contents
4 is What Percent of 19? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to comprehending statistics and financial reports. This in-depth guide will not only answer the question "4 is what percent of 19?" but will also equip you with the knowledge and tools to tackle similar percentage problems with ease. We'll explore multiple methods of solving this problem, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Understanding Percentages
Before diving into the specifics of calculating "4 is what percent of 19?", let's establish a clear understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Percentages are used extensively to represent proportions, changes, and ratios in various contexts. They provide a standardized way to compare different quantities and make data more easily interpretable.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 4 is of 19 involves using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 4 (the value we want to express as a percentage)
- Whole: 19 (the total value)
Let's substitute these values into the formula:
(4 / 19) x 100% = Percentage
Calculating this:
4 / 19 ≈ 0.2105
0.2105 x 100% ≈ 21.05%
Therefore, 4 is approximately 21.05% of 19.
Method 2: Proportion Method
Another approach involves setting up a proportion. We can represent the problem as:
4/19 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
19x = 400
x = 400 / 19
x ≈ 21.05
Therefore, 4 is approximately 21.05% of 19.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function (%) that directly computes percentages. Simply enter "4 ÷ 19 x 100 =" to obtain the result: 21.05%. This method offers the quickest solution, especially for more complex percentage problems.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread applications in various fields. Here are a few examples:
Finance and Budgeting:
- Calculating interest: Determining the interest earned on savings accounts or the interest payable on loans.
- Analyzing financial statements: Understanding profit margins, return on investment (ROI), and other key financial ratios.
- Budgeting and expense tracking: Determining the percentage of income allocated to different expense categories. For instance, you can calculate what percentage of your monthly income is spent on rent, groceries, or transportation.
- Sales tax calculation: Calculating the amount of sales tax added to the price of goods and services.
- Discounts and markdowns: Determining the final price of an item after a percentage discount has been applied.
Statistics and Data Analysis:
- Representing proportions: Expressing the proportion of a particular group within a larger population as a percentage. For example, the percentage of males in a sample population.
- Analyzing survey data: Interpreting survey results by calculating the percentage of respondents who chose specific answers.
- Calculating rates of change: Determining percentage increase or decrease in values over time, like population growth or inflation.
Everyday Life:
- Tip calculation: Determining the appropriate tip amount at restaurants.
- Sales and discounts: Calculating savings on items during sales events.
- Grade calculation: Determining a final grade in a course based on individual assignment percentages.
- Recipe scaling: Adjusting ingredient quantities in a recipe based on percentages. For example, increasing a recipe by 25%.
Beyond the Basic Calculation: Understanding the Context
While knowing the calculation is crucial, understanding the context of the problem is equally important. For instance, if you're determining the percentage of students who passed an exam, a result of 21.05% might signal a significant issue requiring attention. However, if you're calculating the percentage of a specific component in a mixture, 21.05% might be entirely unremarkable depending on the context.
The interpretation of the percentage depends heavily on the specific application. Therefore, always consider the context when interpreting percentage results.
Advanced Percentage Calculations: Dealing with Multiple Percentages
Many real-world scenarios involve multiple percentage calculations. For example, you might encounter situations where you need to calculate the final price after applying successive discounts, or find the overall change after multiple percentage increases or decreases. These require a slightly more nuanced approach, but still build upon the fundamental principles we have already covered.
Here's a brief overview of handling multiple percentages:
-
Successive discounts: When applying multiple discounts, it's crucial to remember that you apply each discount sequentially to the remaining value after the previous discount. Simply adding the discounts together will result in an incorrect calculation.
-
Successive increases/decreases: Similar to successive discounts, you apply each percentage change to the result of the previous change.
-
Combined Percentage Change: When dealing with multiple percentages changes, particularly in complex financial scenarios, understanding the difference between simple and compound interest or growth is vital.
Let's illustrate the issue with successive discounts: A 20% discount followed by a 10% discount is not equivalent to a 30% discount.
Conclusion: Mastering Percentage Calculations
This comprehensive guide has explored various methods for determining what percentage 4 is of 19, ultimately settling on approximately 21.05%. But more importantly, it has equipped you with the fundamental understanding and tools to tackle a wide range of percentage problems, from basic calculations to more complex scenarios involving multiple percentages. Remember, the key to success lies in understanding the underlying principles and applying them appropriately within the given context. By mastering percentage calculations, you significantly enhance your ability to analyze data, make informed decisions, and effectively navigate various aspects of your personal and professional life. Practice these methods consistently, and soon, you'll find calculating percentages becomes second nature.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 24 And 45
May 25, 2025
-
What Is The Gcf Of 18 And 32
May 25, 2025
-
17 Divided By 3 With Remainder
May 25, 2025
-
What Is The Gcf Of 100 And 20
May 25, 2025
-
What Is 0 35 As A Percent
May 25, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 19 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.