What Is 0.35 As A Percent
listenit
May 25, 2025 · 4 min read
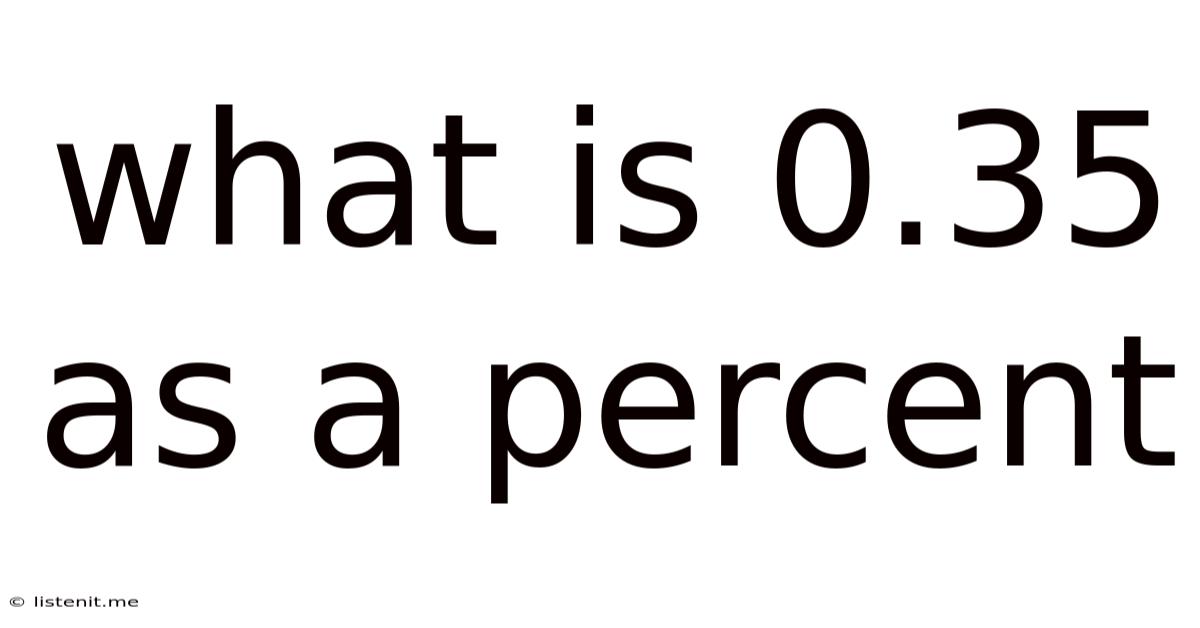
Table of Contents
What is 0.35 as a Percent? A Comprehensive Guide
Converting decimals to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. Understanding this conversion is crucial for interpreting data, calculating discounts, understanding interest rates, and much more. This comprehensive guide will delve into the process of converting 0.35 to a percentage, explaining the underlying concepts and providing practical examples. We'll also explore related concepts and address common misconceptions.
Understanding Decimals and Percentages
Before we tackle the conversion, let's briefly review the definitions of decimals and percentages.
-
Decimals: Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part. For example, 0.35 represents 35/100.
-
Percentages: Percentages represent fractions where the denominator is always 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 35% represents 35/100.
Converting 0.35 to a Percentage: The Simple Method
The conversion from a decimal to a percentage is straightforward. The key is to recognize that a percentage is simply a fraction expressed as parts of 100. To convert a decimal to a percentage, you multiply the decimal by 100 and add the percentage symbol.
Step 1: Multiply by 100
0.35 x 100 = 35
Step 2: Add the Percentage Symbol
35%
Therefore, 0.35 is equal to 35%.
Understanding the Logic Behind the Conversion
The reason multiplying by 100 works is because it effectively changes the denominator of the fraction from a power of 10 to 100. Remember, 0.35 can be written as 35/100. Multiplying by 100 simply transforms this fraction into a percentage:
(35/100) x 100 = 35%
Practical Applications of Decimal to Percentage Conversion
The ability to convert decimals to percentages has numerous real-world applications. Here are a few examples:
-
Calculating Discounts: If a store offers a 0.35 discount on an item, you know it's a 35% discount.
-
Understanding Interest Rates: An annual interest rate of 0.35 means a 35% annual interest rate.
-
Interpreting Data: In statistical analysis, data is often presented as decimals. Converting them to percentages makes the data easier to understand and interpret.
-
Financial Reporting: Financial statements frequently use both decimals and percentages to represent ratios and proportions. Conversion is necessary for clear and effective communication.
-
Grade Calculations: If your score on a test is 0.85, converting this decimal to a percentage (85%) gives you your grade.
Working with Larger and Smaller Decimals
The same method applies regardless of the size of the decimal.
Example 1: Converting 0.05 to a percentage
0.05 x 100 = 5%
Example 2: Converting 1.25 to a percentage
1.25 x 100 = 125%
Note that percentages can be greater than 100%, representing values exceeding the whole.
Converting Percentages to Decimals: The Reverse Process
Often, you might need to perform the reverse operation—converting a percentage back to a decimal. This is equally straightforward. Simply divide the percentage by 100 and remove the percentage symbol.
Example: Convert 35% to a decimal.
35% / 100 = 0.35
Common Misconceptions and Troubleshooting
While the conversion itself is simple, some common misconceptions can arise.
-
Forgetting the Percentage Symbol: Remember to always include the % symbol when expressing a value as a percentage. 35 is not the same as 35%.
-
Incorrect Placement of the Decimal Point: Ensure you're accurately multiplying or dividing by 100. A misplaced decimal point will lead to an incorrect answer.
-
Confusion with Fractions: While decimals and percentages are related to fractions, they are distinct representations. Understanding the relationships between these three forms is essential for accurate conversions.
Advanced Applications and Related Concepts
Beyond the basic conversion, there are several advanced applications and related concepts to consider:
-
Compound Interest: Calculating compound interest involves repeated applications of percentage calculations.
-
Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions and probabilities.
-
Financial Modeling: Building financial models often requires converting between decimals and percentages to accurately represent various financial ratios and indicators.
-
Data Visualization: Presenting data using percentages in charts and graphs often enhances readability and comprehension.
Conclusion: Mastering Decimal-Percentage Conversions
The ability to convert 0.35 to a percentage (35%), and more generally, to convert between decimals and percentages, is a fundamental skill with numerous practical applications. Mastering this skill enhances your ability to interpret data, solve problems, and communicate effectively across various disciplines. By understanding the underlying concepts and practicing the conversion process, you'll confidently navigate this essential aspect of mathematics. Remember to pay close attention to detail, particularly regarding the placement of the decimal point and the inclusion of the percentage symbol. With consistent practice, these conversions will become second nature.
Latest Posts
Latest Posts
-
What Is 2 3 Of 23
May 25, 2025
-
Highest Common Factor Of 15 And 24
May 25, 2025
-
Highest Common Factor Of 10 And 18
May 25, 2025
-
What Are Mortgage Payments On 150 000
May 25, 2025
-
53k A Year Is How Much A Month
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.35 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.