17 Divided By 3 With Remainder
listenit
May 25, 2025 · 5 min read
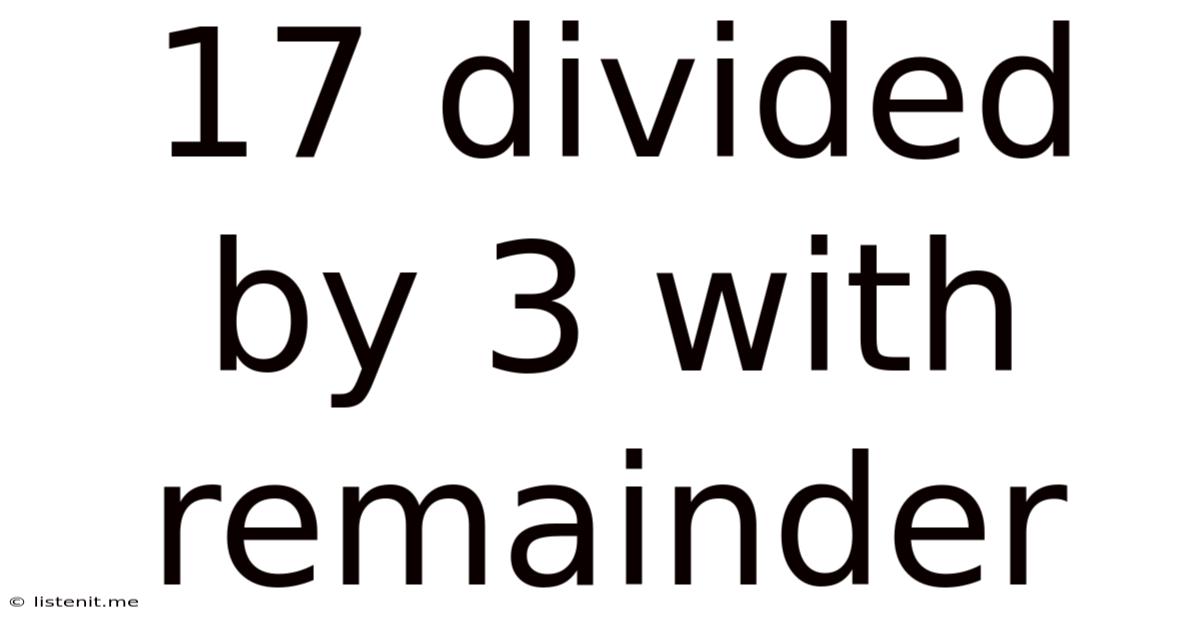
Table of Contents
17 Divided by 3 with Remainder: A Deep Dive into Division and Modular Arithmetic
The seemingly simple question, "What is 17 divided by 3 with a remainder?" opens the door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward, understanding the underlying principles of division, remainders, and their applications extends far beyond basic arithmetic. This article will delve into the mechanics of this specific division problem, explore its broader context within mathematics, and examine its relevance in various fields.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity (the dividend) into equal parts, determined by another quantity (the divisor). When the dividend is not perfectly divisible by the divisor, we're left with a remainder—the portion that's "left over" after the equal division. In the case of 17 divided by 3:
- Dividend: 17
- Divisor: 3
Performing the division, we find that 3 goes into 17 five times (3 x 5 = 15). This leaves a remainder of 2 (17 - 15 = 2). Therefore, 17 divided by 3 is 5 with a remainder of 2.
This can be expressed mathematically as:
17 = 3 * 5 + 2
This equation highlights the core relationship between the dividend, divisor, quotient (the result of the division), and the remainder. This fundamental concept forms the basis of more complex mathematical operations and algorithms.
The Importance of Remainders in Mathematics
Remainders aren't just "leftovers"; they hold significant mathematical weight. They are crucial in several areas:
1. Modular Arithmetic (Clock Arithmetic)
Modular arithmetic, also known as clock arithmetic, deals with remainders after division. It's used extensively in cryptography, computer science, and number theory. Consider a 12-hour clock. If it's 8 o'clock and you add 6 hours, you don't get 14 o'clock; you get 2 o'clock. This is because in modulo 12 arithmetic (mod 12), 14 is equivalent to 2 (14 = 12 * 1 + 2). The remainder is the key.
The remainder of 17 divided by 3 (which is 2) is central to this concept. It represents the "equivalent" value in a system with a modulus of 3. This means 17 is congruent to 2 modulo 3, written as:
17 ≡ 2 (mod 3)
This notation signifies that 17 and 2 have the same remainder when divided by 3.
2. Number Theory and Divisibility Rules
Remainders play a vital role in determining divisibility. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. This rule is based on the concept of remainders. Understanding remainders helps us quickly assess whether a number is divisible by a specific divisor without performing long division.
Similarly, remainders are fundamental in determining prime numbers and exploring concepts like greatest common divisors (GCD) and least common multiples (LCM).
3. Algorithms and Computer Science
Many computer algorithms rely heavily on the concept of remainders. The modulo operator (%) in programming languages directly calculates the remainder of a division. This operator is used in various applications, including:
- Hashing: Generating unique keys for data structures like hash tables.
- Random Number Generation: Ensuring the randomness of generated numbers.
- Cryptography: Implementing encryption and decryption algorithms.
- Data Validation: Checking for valid input values (e.g., ensuring a year is divisible by 4 for leap year calculations).
Applications of Remainders in Real-World Scenarios
The seemingly simple calculation of 17 divided by 3 with a remainder has practical applications across many fields:
1. Resource Allocation
Imagine distributing 17 cookies equally among 3 children. Each child gets 5 cookies (the quotient), and you have 2 cookies left over (the remainder). This simple scenario exemplifies how remainders are essential in resource allocation problems.
2. Scheduling and Time Management
Consider scheduling tasks that repeat every 3 days. If you start a task on day 17, determining the day of the next repetition involves calculating the remainder when 17 is divided by 3. The remainder of 2 indicates the task will next occur on day 2 of the cycle.
3. Manufacturing and Production
Remainders are crucial in manufacturing processes involving the division of materials or the organization of production lines. For instance, if you need to cut 17 meters of fabric into 3-meter pieces, you’ll get 5 pieces and 2 meters remaining.
4. Coding and Data Processing
As previously mentioned, the modulo operator is fundamental in programming and data analysis. It's used to index arrays, cycle through states, and perform various calculations efficiently.
Expanding the Concept: Beyond 17 and 3
While we've focused on 17 divided by 3, the principles discussed apply universally. The process of finding the quotient and remainder when dividing any integer by another integer remains consistent. This fundamental concept underpins more advanced mathematical topics.
Exploring Different Division Methods
While long division is a common method, several techniques can be used to find the quotient and remainder:
-
Repeated Subtraction: Repeatedly subtract the divisor (3) from the dividend (17) until you reach a value less than the divisor. The number of subtractions is the quotient, and the final value is the remainder.
-
Division Algorithm: The division algorithm formally states that for any integers a (dividend) and b (divisor) with b > 0, there exist unique integers q (quotient) and r (remainder) such that a = bq + r, and 0 ≤ r < b.
-
Using a Calculator: Modern calculators often have a modulo function (%) that directly calculates the remainder.
Conclusion: The Power of Remainders
The seemingly insignificant remainder of 2 when 17 is divided by 3 reveals the depth and importance of this fundamental mathematical concept. From the elegant world of number theory to the practical applications in computer science and everyday life, understanding remainders provides valuable insights and tools. Its application extends far beyond basic arithmetic, empowering us to solve complex problems and appreciate the intricate beauty of mathematics. The next time you encounter a division problem, remember the often overlooked, but powerful, remainder. Its subtle presence holds the key to unlocking deeper mathematical understanding and problem-solving capabilities. The simple act of dividing 17 by 3 serves as a gateway to a rich mathematical landscape, showcasing the interconnectedness of mathematical concepts and their practical relevance in our world.
Latest Posts
Latest Posts
-
1979 To Now How Many Years
May 25, 2025
-
52 000 A Year Is How Much Biweekly
May 25, 2025
-
What Is The Greatest Common Factor Of 27 And 72
May 25, 2025
-
Highest Common Factor Of 20 And 24
May 25, 2025
-
Convert 71 2 3 To A Fraction In Lowest Terms
May 25, 2025
Related Post
Thank you for visiting our website which covers about 17 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.