38 Out Of 55 As A Percentage
listenit
May 24, 2025 · 5 min read
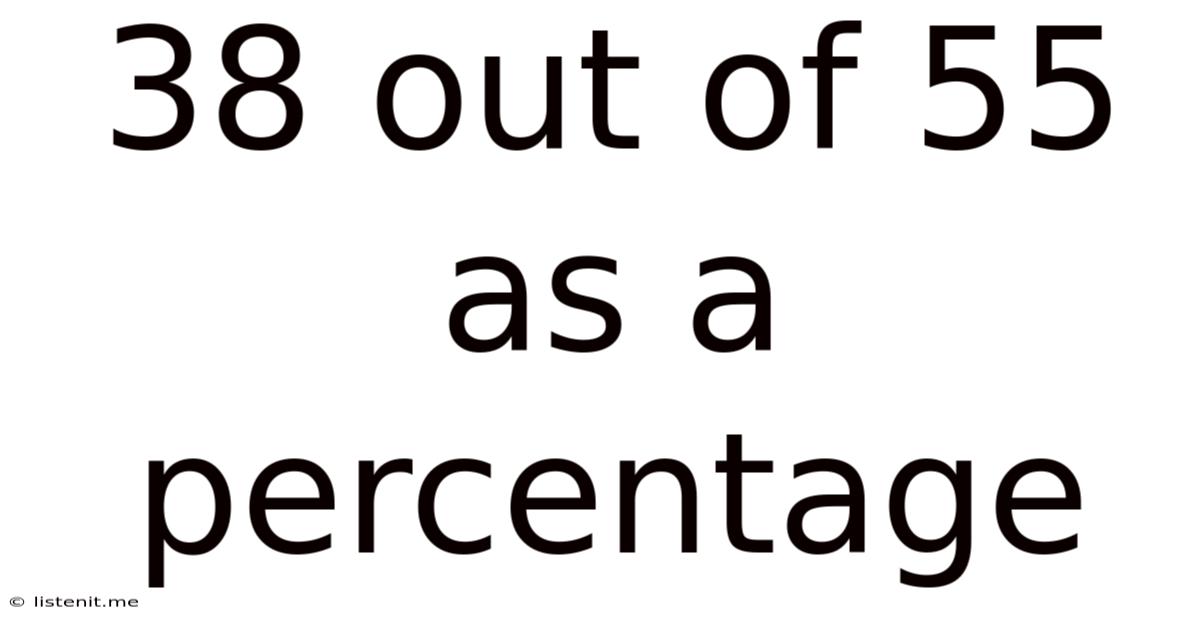
Table of Contents
38 out of 55 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications across various fields, from finance and academics to everyday life. Understanding how to convert fractions and ratios into percentages allows for easier comparisons and analysis of data. This article delves into the specific calculation of 38 out of 55 as a percentage, providing a detailed explanation, practical examples, and exploring related percentage concepts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion of a whole, with the whole always being considered as 100%.
For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Similarly, 25% represents 25 out of 100, equivalent to 1/4 or 0.25. Understanding this fundamental concept is crucial for tackling percentage calculations.
Calculating 38 out of 55 as a Percentage
To determine what percentage 38 represents out of 55, we follow a straightforward method:
-
Form a fraction: Express the given numbers as a fraction: 38/55. This fraction represents the portion (38) relative to the whole (55).
-
Convert the fraction to a decimal: Divide the numerator (38) by the denominator (55): 38 ÷ 55 ≈ 0.6909
-
Convert the decimal to a percentage: Multiply the decimal result by 100: 0.6909 × 100 ≈ 69.09%
Therefore, 38 out of 55 is approximately 69.09%.
Different Methods for Calculating Percentages
While the above method is the most common, there are alternative approaches to calculate percentages, each with its own advantages depending on the context and personal preference.
-
Using Proportions: We can set up a proportion to solve for the unknown percentage (x):
38/55 = x/100
Cross-multiplying gives: 55x = 3800
Solving for x: x = 3800/55 ≈ 69.09%
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the process. Simply enter 38 ÷ 55 × 100 to directly obtain the percentage.
-
Mental Estimation: For quick approximations, rounding numbers can be helpful. Rounding 38 to 40 and 55 to 50, we get 40/50 = 0.8 or 80%. While this isn't precise, it provides a reasonable estimate for quick assessments.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in a wide range of real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage changes is vital for analyzing financial trends and making informed decisions.
-
Academics: Assessing grades, determining test scores, and calculating overall performance metrics. Percentages are used extensively to represent academic achievements and progress.
-
Statistics: Percentages are fundamental for summarizing and presenting data, expressing probabilities, and conducting statistical analyses. They help make complex data more understandable and accessible.
-
Retail: Calculating discounts, sales tax, and markups. Businesses use percentages heavily in pricing strategies, promotions, and inventory management.
-
Science: Expressing concentrations, error margins, and data variations in experiments and research. Percentages provide a standardized way to represent quantitative relationships in scientific studies.
-
Everyday Life: Calculating tips, splitting bills, understanding nutritional information on food labels, and interpreting various statistical information encountered daily.
Beyond the Basics: Understanding Percentage Change and Percentage Increase/Decrease
While calculating a percentage from a fraction or ratio is fundamental, understanding percentage change is equally important. Percentage change shows the relative difference between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a stock price increased from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
Similarly, a percentage decrease shows the relative reduction between two values. If the stock price dropped from $60 to $48, the percentage decrease is:
[(48 - 60) / 60] x 100% = -20%
Advanced Percentage Applications: Compound Interest and Discounts
Percentage calculations become more complex when dealing with compound interest or multiple discounts.
- Compound Interest: Compound interest calculates interest not just on the principal amount but also on accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
where:
A = the future value of the investment/loan, including interest P = the principal investment amount (the initial deposit or loan amount) r = the annual interest rate (decimal) n = the number of times that interest is compounded per year t = the number of years the money is invested or borrowed for
- Multiple Discounts: When multiple discounts are applied sequentially, the calculations require careful attention to order of operations. A 20% discount followed by a 10% discount is not equivalent to a single 30% discount. The final price will be lower with sequential discounts.
Troubleshooting Common Percentage Calculation Mistakes
Even seemingly simple percentage calculations can be prone to errors. Here are some common mistakes to avoid:
-
Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Confusing Percentage Increase/Decrease: Ensure that you correctly identify the old and new values when calculating percentage changes.
-
Incorrect Decimal Placement: Pay close attention to decimal points when converting between decimals and percentages.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations or financial applications where precision is critical.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is essential for various aspects of life. Understanding the fundamental concepts, different calculation methods, and potential pitfalls ensures accurate and efficient problem-solving. Whether applying percentages to financial planning, academic performance analysis, or everyday decision-making, a solid understanding of percentages will prove invaluable. By consistently practicing and applying the techniques discussed in this article, you can build confidence and competence in tackling percentage-related challenges. Remember to always double-check your calculations and consider using different methods to verify your answers. This thorough approach will enhance accuracy and solidify your understanding of this fundamental mathematical skill.
Latest Posts
Latest Posts
-
What Is The Gcf Of 39 And 52
May 25, 2025
-
4 Out Of 22 As A Percentage
May 25, 2025
-
Como Saber Mi Gpa En Estados Unidos
May 25, 2025
-
What Is 5 And 1 4 As A Decimal
May 25, 2025
-
How Long Ago Was 50 Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about 38 Out Of 55 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.