What Is The Gcf Of 39 And 52
listenit
May 25, 2025 · 5 min read
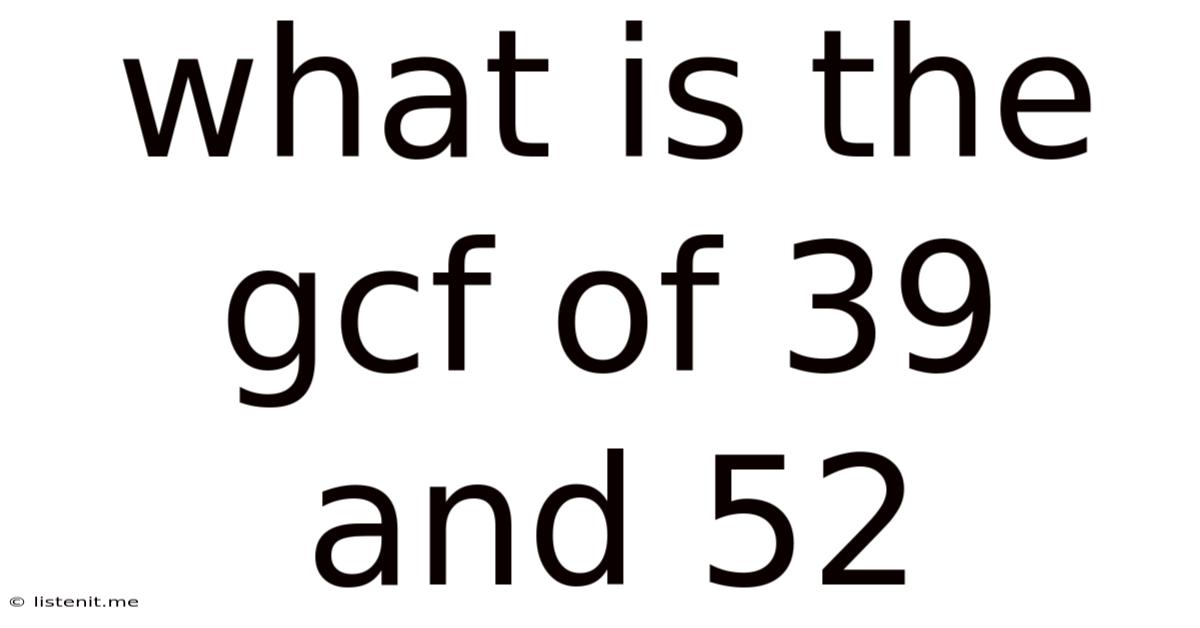
Table of Contents
What is the GCF of 39 and 52? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and various methods for solving it opens doors to a deeper appreciation of number theory and its applications in various fields. This comprehensive guide will explore different ways to determine the GCF of 39 and 52, offering insights beyond a simple answer. We'll cover the prime factorization method, the Euclidean algorithm, and even discuss the significance of GCF in real-world scenarios.
Understanding the Greatest Common Factor (GCF)
Before we dive into finding the GCF of 39 and 52, let's clarify what the GCF actually is. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. Understanding this definition is crucial to applying the various methods we'll discuss.
Method 1: Prime Factorization
This is perhaps the most intuitive method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 39 and 52:
Prime Factorization of 39:
39 can be broken down as follows:
- 39 = 3 x 13
Both 3 and 13 are prime numbers.
Prime Factorization of 52:
52 can be broken down as follows:
- 52 = 2 x 2 x 13 = 2² x 13
Here, 2 and 13 are the prime factors.
Finding the GCF using Prime Factorization:
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. In this case:
- The common prime factor is 13.
- The lowest power of 13 is 13¹ (or simply 13).
Therefore, the GCF of 39 and 52 is 13.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 39 and 52:
-
Start with the larger number (52) and the smaller number (39): 52 and 39
-
Subtract the smaller number from the larger number: 52 - 39 = 13
-
Replace the larger number with the result (13) and keep the smaller number (39): 39 and 13
-
Repeat the subtraction: 39 - 13 = 26
-
Repeat again: 26 - 13 = 13
-
Repeat again: 13 - 13 = 0
When the difference becomes 0, the last non-zero result is the GCF. Therefore, the GCF of 39 and 52 is 13.
Method 3: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 39:
1, 3, 13, 39
Factors of 52:
1, 2, 4, 13, 26, 52
Identifying the Common Factors:
Comparing the lists, we see that the common factors are 1 and 13. The largest of these is 13. Therefore, the GCF of 39 and 52 is 13. This method becomes less efficient with larger numbers.
Applications of the GCF in Real-World Scenarios
The concept of GCF finds practical applications in various fields:
-
Simplifying Fractions: Finding the GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 39/52 can be simplified to 3/4 by dividing both the numerator and denominator by their GCF, which is 13.
-
Geometry and Measurement: GCF is used in problems involving area and perimeter calculations. For instance, when dividing a rectangular area into smaller, equally sized squares, the side length of the squares must be a common factor of the rectangle's dimensions. The largest possible square size is determined by the GCF.
-
Project Management and Resource Allocation: Consider scenarios where you need to divide resources or tasks equally among groups. The GCF helps determine the largest possible equal allocation. For example, if you have 39 apples and 52 oranges and want to divide them into identical bags, you can create 13 bags, each with 3 apples and 4 oranges.
-
Cryptography: GCF plays a vital role in some cryptographic algorithms, particularly in tasks related to modular arithmetic and finding the multiplicative inverse.
Beyond the Basics: Understanding the Implications of Relatively Prime Numbers
When the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1. For example, while 39 and 52 are not relatively prime (their GCF is 13), the numbers 15 and 28 are relatively prime (their GCF is 1). Understanding relatively prime numbers is important in various mathematical concepts and applications.
Conclusion: Mastering GCF for Enhanced Mathematical Proficiency
Finding the GCF of 39 and 52, as we've demonstrated, can be achieved through several methods. The choice of method depends on the size of the numbers and personal preference. While the prime factorization method provides a clear visual understanding of the factors, the Euclidean algorithm proves more efficient for larger numbers. The listing factors method is suitable for smaller numbers but becomes cumbersome with larger values. Regardless of the method used, the GCF of 39 and 52 consistently comes out as 13. This seemingly simple calculation, however, showcases fundamental principles of number theory and highlights its significant role in various practical applications, emphasizing the importance of mastering this concept for broader mathematical proficiency. Understanding GCF enhances problem-solving skills and contributes to a deeper appreciation of mathematical relationships and their real-world relevance.
Latest Posts
Latest Posts
-
5 1 4 As A Decimal
May 25, 2025
-
9 1 3 As An Improper Fraction
May 25, 2025
-
What Is 30 Divided By 5
May 25, 2025
-
8 1 5 As An Improper Fraction
May 25, 2025
-
How Many Calories Are In 1 Point For Weight Watchers
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 39 And 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.