3 5 6 As An Improper Fraction
listenit
Mar 25, 2025 · 5 min read
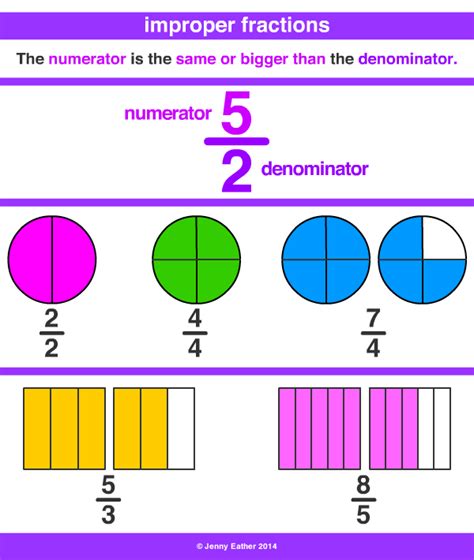
Table of Contents
- 3 5 6 As An Improper Fraction
- Table of Contents
- 3 5/6 as an Improper Fraction: A Comprehensive Guide
- Understanding Mixed Numbers and Improper Fractions
- Converting 3 5/6 to an Improper Fraction: A Step-by-Step Approach
- Visualizing the Conversion
- Practical Applications of Improper Fractions
- Further Exploration: Converting Improper Fractions Back to Mixed Numbers
- Advanced Applications and Problem Solving
- Conclusion: Mastering Improper Fractions for Mathematical Proficiency
- Latest Posts
- Latest Posts
- Related Post
3 5/6 as an Improper Fraction: A Comprehensive Guide
Understanding fractions is a cornerstone of mathematics, crucial for various applications from basic arithmetic to advanced calculus. Within the realm of fractions, improper fractions often present a unique challenge, particularly for those transitioning from simpler fraction concepts. This comprehensive guide will explore the concept of improper fractions, focusing specifically on converting the mixed number 3 5/6 into its improper fraction equivalent. We will delve into the underlying principles, provide step-by-step instructions, and explore practical applications to solidify your understanding.
Understanding Mixed Numbers and Improper Fractions
Before we dive into converting 3 5/6, let's establish a clear understanding of mixed numbers and improper fractions.
Mixed numbers consist of a whole number and a proper fraction. A proper fraction has a numerator (the top number) smaller than its denominator (the bottom number). For example, 3 5/6 is a mixed number: 3 represents the whole number, and 5/6 represents the proper fraction.
Improper fractions, on the other hand, have a numerator that is equal to or greater than the denominator. Examples include 7/4, 11/5, and 23/6. While seemingly more complex, improper fractions are a fundamental building block in many mathematical operations. They provide a more concise and often easier-to-manipulate representation for calculations involving fractions.
Converting 3 5/6 to an Improper Fraction: A Step-by-Step Approach
Converting a mixed number like 3 5/6 to an improper fraction involves a straightforward process. Here's a step-by-step guide:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 3, and the denominator is 6. Therefore, we calculate 3 * 6 = 18.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 5. We add this to the result from Step 1: 18 + 5 = 23.
Step 3: Keep the denominator the same.
The denominator remains unchanged throughout this process. The denominator in 3 5/6 is 6, so our improper fraction will also have a denominator of 6.
Step 4: Write the improper fraction.
Combining the results from Steps 2 and 3, we get our improper fraction: 23/6.
Therefore, 3 5/6 is equivalent to the improper fraction 23/6.
Visualizing the Conversion
It can be helpful to visualize the conversion process. Imagine having three whole pizzas, each cut into six slices. The mixed number 3 5/6 represents three whole pizzas and five additional slices from a fourth pizza. To express this as an improper fraction, we need to count all the slices. Each pizza has six slices, so three pizzas have 3 * 6 = 18 slices. Adding the five extra slices gives us a total of 18 + 5 = 23 slices. Since each slice represents 1/6 of a pizza, we have 23/6 slices in total, confirming our conversion.
Practical Applications of Improper Fractions
Improper fractions aren't just theoretical constructs; they have many practical applications in various fields:
-
Baking and Cooking: Recipes often require fractional amounts of ingredients. Converting mixed numbers to improper fractions simplifies calculations when combining or scaling recipes. For instance, if a recipe calls for 1 3/4 cups of flour and you want to double the recipe, converting 1 3/4 to 7/4 makes the doubling process (14/4) much easier.
-
Construction and Engineering: Accurate measurements are critical in construction and engineering. Improper fractions provide precise representation of measurements, particularly when working with fractions of inches or meters.
-
Finance and Accounting: Calculating interest, profits, or losses often involves working with fractions. Converting between mixed numbers and improper fractions helps in performing accurate financial calculations.
-
Data Analysis and Statistics: Improper fractions are commonly used in various statistical calculations, offering a more streamlined way to represent proportions and ratios.
-
Computer Programming: Many programming languages require numerical inputs, and using improper fractions ensures accuracy in calculations involving fractional values.
Further Exploration: Converting Improper Fractions Back to Mixed Numbers
Just as we can convert mixed numbers to improper fractions, we can perform the reverse operation. Converting an improper fraction back to a mixed number helps in understanding and interpreting the value of the fraction in a more relatable way.
To convert an improper fraction (like 23/6) back into a mixed number, follow these steps:
Step 1: Divide the numerator by the denominator.
23 divided by 6 is 3 with a remainder of 5.
Step 2: The quotient becomes the whole number.
The quotient (3) becomes the whole number part of the mixed number.
Step 3: The remainder becomes the numerator of the proper fraction.
The remainder (5) becomes the numerator of the proper fraction.
Step 4: The denominator remains the same.
The denominator remains 6.
Step 5: Write the mixed number.
Combining the whole number and the proper fraction, we get the mixed number 3 5/6, confirming the reversibility of the conversion.
Advanced Applications and Problem Solving
Understanding the conversion between mixed numbers and improper fractions is essential for tackling more complex mathematical problems. For example, when adding or subtracting fractions with different denominators, converting them to improper fractions with a common denominator often simplifies the process. Similarly, when multiplying or dividing fractions, working with improper fractions can make the calculations more efficient and less prone to errors.
Conclusion: Mastering Improper Fractions for Mathematical Proficiency
Mastering the conversion of mixed numbers to improper fractions is a fundamental skill for anyone pursuing mathematical proficiency. This guide has provided a clear, step-by-step method for converting 3 5/6 to its improper fraction equivalent (23/6), accompanied by visual aids and practical applications to solidify understanding. Remember to practice regularly to build your confidence and accuracy in working with fractions. This fundamental skill will benefit you not only in academic settings but also in various real-world scenarios, demonstrating the practical relevance of this seemingly simple mathematical concept. By understanding and utilizing improper fractions effectively, you’ll unlock a deeper understanding of mathematics and its power in problem-solving.
Latest Posts
Latest Posts
-
How To Find Inverse Of An Exponential Function
Mar 29, 2025
-
Determine The Rate Law For The Overall Reaction
Mar 29, 2025
-
Sum And Or Difference Of Logarithms
Mar 29, 2025
-
Simplify The Square Root Of 84
Mar 29, 2025
-
What Is The Lcm Of 14 And 10
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about 3 5 6 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
