3 1/4 Divided By 3 As A Fraction
listenit
May 09, 2025 · 5 min read
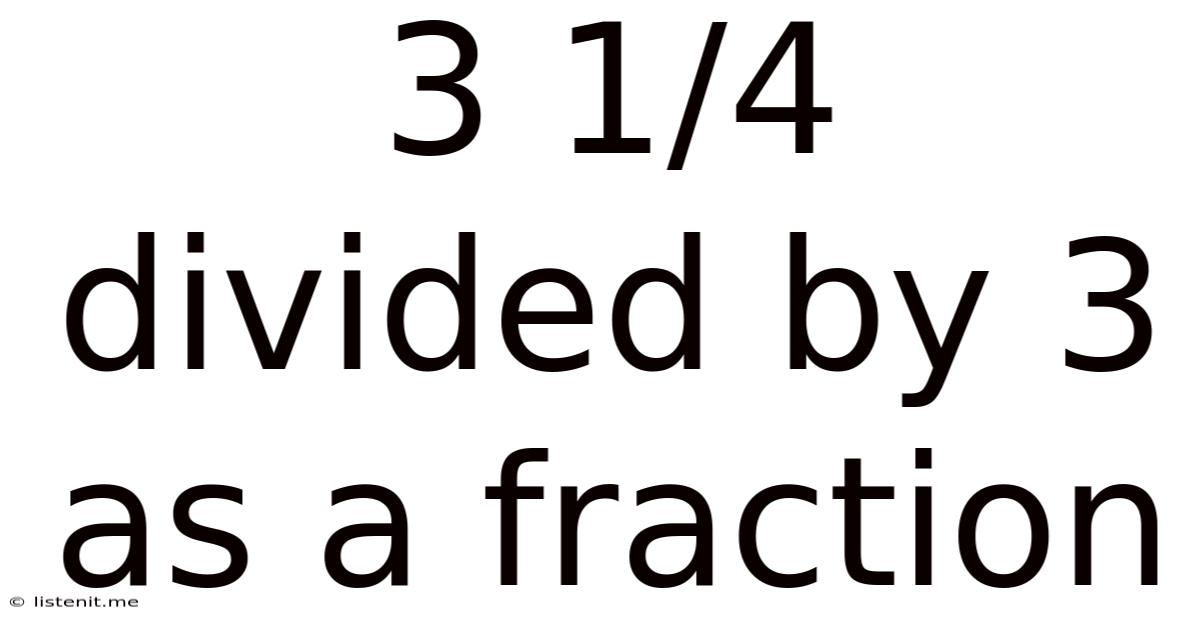
Table of Contents
3 1/4 Divided by 3 as a Fraction: A Comprehensive Guide
Understanding fractions and how to perform operations on them is a fundamental skill in mathematics. This guide will walk you through the process of dividing the mixed number 3 1/4 by 3, explaining the steps clearly and offering insights into the underlying principles. We'll explore various methods, ensuring a comprehensive understanding for students and anyone looking to refresh their fractional arithmetic skills.
Converting Mixed Numbers to Improper Fractions
Before we begin the division, we need to convert the mixed number 3 1/4 into an improper fraction. A mixed number combines a whole number and a fraction (e.g., 3 1/4). An improper fraction has a numerator larger than or equal to its denominator (e.g., 13/4).
The conversion process:
- Multiply the whole number by the denominator: 3 x 4 = 12
- Add the numerator to the result: 12 + 1 = 13
- Keep the same denominator: 4
Therefore, 3 1/4 is equivalent to the improper fraction 13/4.
Method 1: Dividing Fractions Directly
Now that we have 13/4, we can proceed with the division. Dividing by 3 is the same as multiplying by its reciprocal (1/3). The reciprocal of a number is simply 1 divided by that number.
The steps:
- Rewrite the division as multiplication: (13/4) ÷ 3 = (13/4) x (1/3)
- Multiply the numerators together: 13 x 1 = 13
- Multiply the denominators together: 4 x 3 = 12
- Simplify the resulting fraction: 13/12
The answer, 13/12, is an improper fraction. We can convert it back to a mixed number if desired.
Converting Improper Fractions to Mixed Numbers
To convert the improper fraction 13/12 back to a mixed number:
- Divide the numerator by the denominator: 13 ÷ 12 = 1 with a remainder of 1
- The whole number part is the quotient: 1
- The fractional part is the remainder over the denominator: 1/12
Therefore, 13/12 is equivalent to the mixed number 1 1/12.
Method 2: Dividing the Whole and Fractional Parts Separately (Alternative Approach)
This method provides a different perspective on the problem. It involves separating the mixed number into its whole and fractional parts before division.
The steps:
- Separate the mixed number: 3 1/4 can be written as 3 + 1/4
- Divide each part by 3: (3 ÷ 3) + (1/4 ÷ 3)
- Simplify: 1 + (1/4 x 1/3) = 1 + 1/12
- Combine the whole number and fraction: 1 + 1/12 = 1 1/12
This method demonstrates the distributive property of division, showing that dividing a mixed number by a number is the same as dividing each part of the mixed number separately and then summing the results.
Understanding the Significance of Simplification
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret. 13/12 is less intuitive than 1 1/12.
- Efficiency: Simplified fractions are more efficient for further calculations.
- Standard Form: Presenting answers in simplified form is a standard mathematical practice.
Always check if your final fraction can be simplified. In this case, 13/12 cannot be simplified further because 13 and 12 share no common factors other than 1.
Practical Applications and Real-World Examples
The concept of dividing fractions, particularly mixed numbers, has many practical applications in various fields:
- Cooking and Baking: Scaling recipes up or down often requires dividing fractional amounts of ingredients.
- Construction and Engineering: Precise measurements and calculations using fractions are essential in construction projects.
- Sewing and Tailoring: Cutting fabric accurately requires understanding and working with fractions.
- Data Analysis: Working with data sets often involves calculating averages and proportions, which frequently involve fractional arithmetic.
Understanding this concept is essential for anyone working in fields requiring precise measurements or calculations.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing mixed numbers:
- Incorrect conversion to improper fraction: Failure to correctly convert the mixed number to an improper fraction before division is a frequent error. Always double-check this step.
- Forgetting the reciprocal: Remember to multiply by the reciprocal of the divisor, not the divisor itself.
- Incorrect simplification: Make sure to simplify the resulting fraction to its lowest terms.
- Arithmetic errors: Carefully perform the multiplication and addition operations to avoid simple calculation mistakes.
By paying close attention to these details, you can minimize errors and ensure accuracy in your calculations.
Advanced Concepts and Extensions
This fundamental concept can be expanded upon to explore more complex scenarios:
- Dividing by Fractions: This guide focuses on dividing by a whole number, but the same principles apply when dividing by a fraction.
- Dividing Multiple Mixed Numbers: The principles can be extended to problems involving multiple mixed numbers.
- Applications in Algebra: Fractions and mixed numbers play a significant role in algebraic equations and problem-solving.
Mastering these fundamental concepts opens doors to more advanced mathematical topics.
Conclusion: Mastering Fraction Division
Dividing a mixed number like 3 1/4 by 3, resulting in the fraction 13/12 or the mixed number 1 1/12, is a crucial skill in mathematics. Understanding the process, from converting mixed numbers to improper fractions, performing the division, and simplifying the result, is essential for various applications. By carefully following the steps and understanding the underlying principles, you can confidently tackle similar problems and apply this knowledge to real-world situations. Remember to always double-check your work and practice regularly to build fluency and accuracy. This comprehensive guide provides a solid foundation for mastering fraction division and furthering your mathematical skills. Consistent practice is key to developing proficiency in this fundamental area of mathematics. Remember to break down complex problems into smaller, manageable steps, and always double-check your calculations.
Latest Posts
Latest Posts
-
Determine Whether The Proportion Is True Or False
May 09, 2025
-
The Base Unit For Mass Is The
May 09, 2025
-
Through 4 2 Parallel To Y 3 4x 5
May 09, 2025
-
Earth Rotates From West To East
May 09, 2025
-
Whats Half Of 1 And 1 4
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 1/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.