Through 4 2 Parallel To Y 3 4x 5
listenit
May 09, 2025 · 5 min read
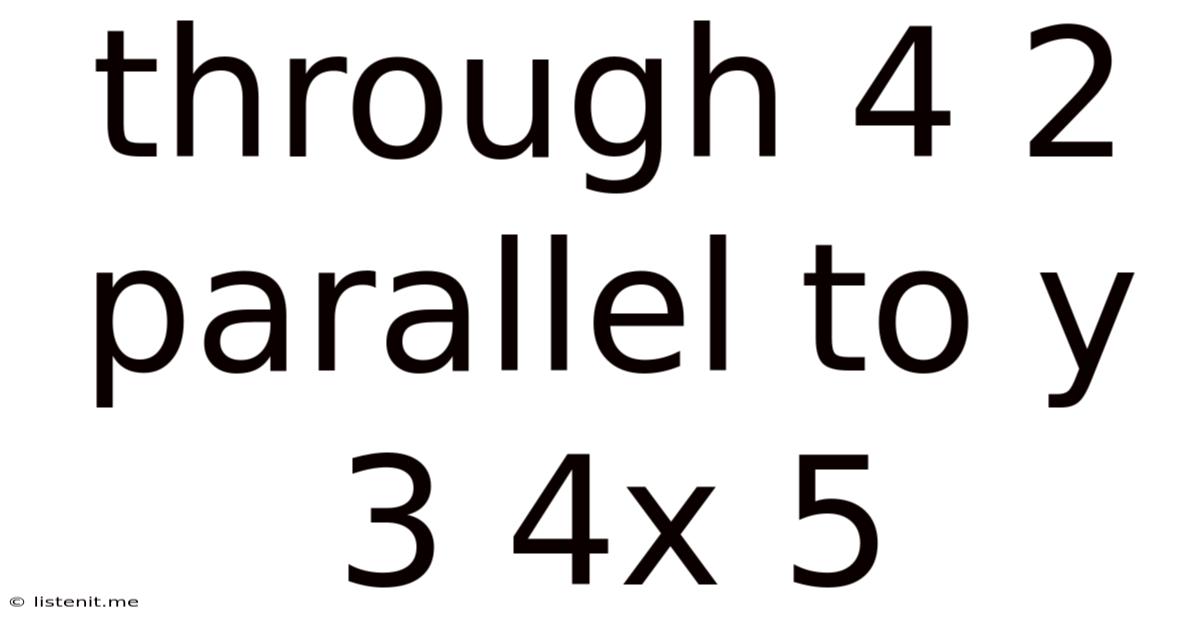
Table of Contents
Through the Line: Analyzing the Parallel Line y = 3/4x + 5
This article delves into the mathematical concept of parallel lines, specifically focusing on the line parallel to y = (3/4)x + 5 and passing through the point (4, 2). We'll explore the underlying principles, the step-by-step process of finding the equation of this parallel line, and finally, broaden the discussion to encompass related concepts and applications.
Understanding Parallel Lines
Parallel lines are lines in a plane that never meet, regardless of how far they are extended. This fundamental geometric property stems from their equal slopes. The slope of a line, often represented by 'm', represents the steepness or inclination of the line. It's calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line.
Key Characteristic of Parallel Lines: Parallel lines always have the same slope. This is crucial for identifying and constructing parallel lines. If two lines have different slopes, they will eventually intersect.
Finding the Equation of the Parallel Line
Our goal is to find the equation of the line that is parallel to y = (3/4)x + 5 and passes through the point (4, 2).
1. Identifying the Slope:
The given line, y = (3/4)x + 5, is in slope-intercept form (y = mx + b), where 'm' is the slope and 'b' is the y-intercept. Therefore, the slope of this line is m = 3/4. Since parallel lines share the same slope, the slope of our target line is also 3/4.
2. Utilizing the Point-Slope Form:
The point-slope form of a linear equation is an excellent tool for finding the equation of a line when we know its slope and a point it passes through. The formula is:
y - y₁ = m(x - x₁)
where:
- 'm' is the slope
- (x₁, y₁) is the given point
3. Substituting Values:
We know the slope (m = 3/4) and the point (x₁ = 4, y₁ = 2). Substituting these values into the point-slope form, we get:
y - 2 = (3/4)(x - 4)
4. Simplifying to Slope-Intercept Form:
To obtain the equation in the more familiar slope-intercept form (y = mx + b), we simplify the equation:
y - 2 = (3/4)x - 3 y = (3/4)x - 3 + 2 y = (3/4)x - 1
Therefore, the equation of the line parallel to y = (3/4)x + 5 and passing through the point (4, 2) is y = (3/4)x - 1.
Graphical Representation
Visualizing these lines on a graph solidifies our understanding. Both lines will have the same inclination (slope), but they will be separated by a vertical distance. The y-intercept – the point where the line crosses the y-axis – will be different for each line. The line y = (3/4)x + 5 intercepts the y-axis at 5, while the parallel line y = (3/4)x - 1 intercepts at -1.
Extending the Concept: Perpendicular Lines
While we focused on parallel lines, it's valuable to understand the relationship between parallel and perpendicular lines. Perpendicular lines intersect at a right angle (90 degrees). The slopes of perpendicular lines have a specific relationship: they are negative reciprocals of each other.
If the slope of a line is 'm', the slope of a line perpendicular to it is '-1/m'. For instance, a line perpendicular to y = (3/4)x + 5 would have a slope of -4/3.
Real-World Applications
The concept of parallel lines has numerous applications in various fields:
-
Architecture and Engineering: Parallel lines are fundamental in structural design, ensuring stability and alignment in buildings and bridges. Parallel beams and supports are crucial for distributing weight effectively.
-
Computer Graphics: In computer-aided design (CAD) and other graphics software, parallel lines are essential for creating accurate and consistent representations of objects and scenes.
-
Cartography: Mapmaking relies on parallel lines of latitude and longitude to accurately represent locations on the Earth's surface.
-
Physics: In physics, parallel forces and parallel vectors are often encountered in mechanics and other areas.
-
Everyday Life: We encounter parallel lines in everyday objects, from railway tracks and window frames to lines on a notebook page.
Advanced Concepts and Further Exploration
This basic understanding of parallel lines can be expanded upon through more advanced mathematical concepts:
-
Vectors: Lines can be represented using vectors, allowing for a more abstract and generalized approach to parallel line analysis.
-
Linear Algebra: Linear algebra provides a powerful framework for dealing with systems of linear equations and geometric transformations involving parallel lines.
-
Calculus: Concepts related to parallel lines, like tangents and slopes, are fundamental in calculus.
-
Analytic Geometry: Analytic geometry allows us to describe and analyze geometric figures using algebraic equations, providing a powerful tool for studying parallel lines within a coordinate system.
Conclusion
Understanding the concept of parallel lines and determining the equation of a line parallel to a given line is a fundamental skill in mathematics. This article has provided a comprehensive exploration of this concept, from the basic definition of parallel lines and their properties to more advanced applications and related mathematical concepts. Mastering this understanding lays a strong foundation for tackling more complex mathematical problems and opens doors to applications in diverse fields. The ability to analyze and work with parallel lines is an essential tool for anyone pursuing studies or careers in mathematics, engineering, computer science, or any field involving geometry and spatial reasoning. The key takeaway is the importance of the slope as the defining characteristic of parallel lines, and the power of the point-slope form in determining the equation of a specific parallel line given a point and the slope of a parallel line.
Latest Posts
Latest Posts
-
69 As A Fraction In Simplest Form
May 09, 2025
-
What Is 64 Divided By 8
May 09, 2025
-
Find Limit As X Approaches 0
May 09, 2025
-
2 3 Divided By 1 3 As A Fraction
May 09, 2025
-
How Many Orbitals In N 5
May 09, 2025
Related Post
Thank you for visiting our website which covers about Through 4 2 Parallel To Y 3 4x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.