28 Is 40 Percent Of What Number
listenit
May 12, 2025 · 5 min read
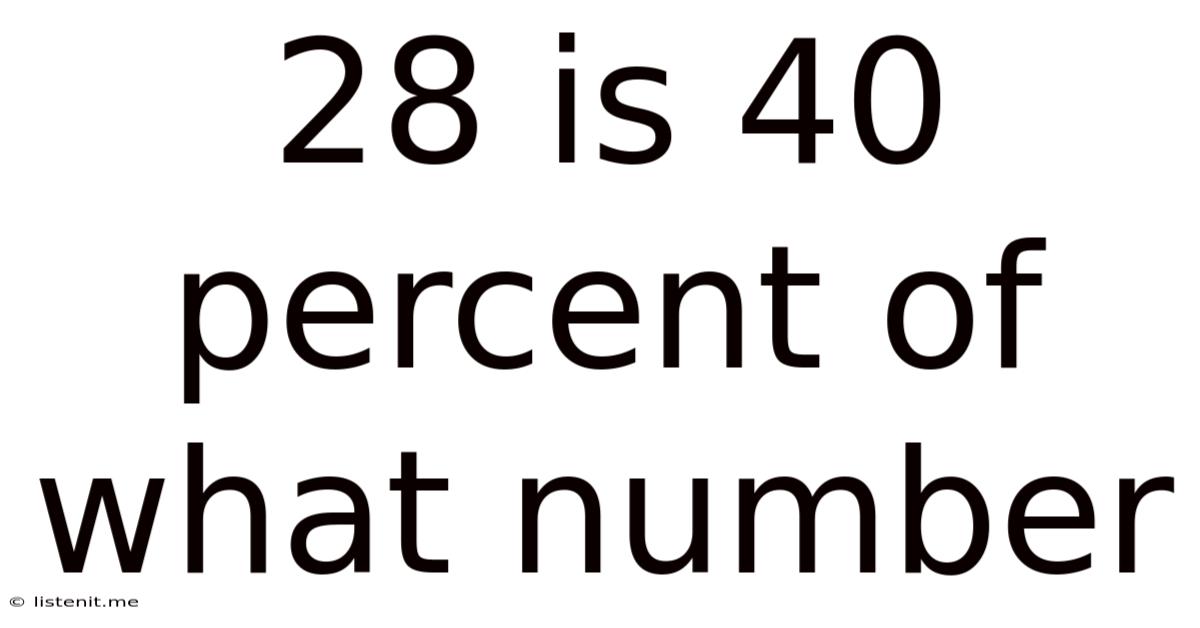
Table of Contents
28 is 40 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Finding an unknown number when you know a percentage of it is a common problem in mathematics, appearing frequently in various fields like finance, statistics, and everyday life. Let's delve into how to solve the problem "28 is 40 percent of what number?" and explore the broader context of percentage calculations. This guide will not only provide the solution but also equip you with the understanding and tools to tackle similar problems independently.
Understanding Percentages
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 40% means 40 out of 100, or 40/100, which simplifies to 2/5. This representation is crucial for solving percentage problems.
Method 1: Using the Equation
The most straightforward approach to solving "28 is 40 percent of what number?" is using a simple algebraic equation. Let's represent the unknown number as 'x'. We can translate the problem into an equation:
28 = 0.40 * x
Here's how to solve for 'x':
-
Convert the percentage to a decimal: 40% becomes 0.40 (divide by 100).
-
Substitute into the equation: This gives us 28 = 0.40x.
-
Isolate 'x': Divide both sides of the equation by 0.40: x = 28 / 0.40
-
Calculate the result: x = 70
Therefore, 28 is 40 percent of 70.
Method 2: Using Proportions
Proportions offer another effective method for solving percentage problems. A proportion establishes an equivalence between two ratios. We can set up a proportion as follows:
28/x = 40/100
This proportion states that the ratio of 28 to the unknown number (x) is equal to the ratio of 40 to 100.
To solve for x:
-
Cross-multiply: This gives us 28 * 100 = 40 * x, which simplifies to 2800 = 40x.
-
Isolate 'x': Divide both sides by 40: x = 2800 / 40
-
Calculate the result: x = 70
Again, we find that 28 is 40 percent of 70.
Method 3: Working Backwards from the Percentage
This method involves a more intuitive approach. If 28 represents 40% of a number, then we can find 10% by dividing 28 by 4:
28 / 4 = 7
Since 10% is 7, we can then find 100% (the whole number) by multiplying by 10:
7 * 10 = 70
Thus, we arrive at the same answer: 28 is 40 percent of 70.
Practical Applications: Real-World Examples
Understanding percentage calculations is essential in various real-world situations:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all involve percentage calculations. For example, determining the original price of an item after a 40% discount requires using the principles discussed above.
-
Statistics: Percentages are fundamental in representing data and analyzing trends. For instance, calculating the percentage of respondents who prefer a particular product or service requires accurate percentage calculations.
-
Everyday Life: We encounter percentages daily in tipping situations at restaurants, calculating sales tax, understanding nutritional information on food labels (e.g., percentage of daily value for nutrients), and interpreting statistics in news reports.
Expanding the Understanding: Variations on the Problem
Let's explore some variations on the core problem to further strengthen your understanding:
Scenario 1: Finding the Percentage
What if the question was: "28 is what percent of 70?"
To solve this, we'd use the formula: (Part/Whole) * 100%
(28/70) * 100% = 40%
Scenario 2: Finding the Part
What if the question was: "What is 40% of 70?"
To solve this, we'd simply multiply 70 by 0.40:
70 * 0.40 = 28
Scenario 3: More Complex Percentages
Let's consider a more complex scenario: "35 is 17.5% of what number?"
Using the equation method:
35 = 0.175x x = 35 / 0.175 x = 200
Therefore, 35 is 17.5% of 200.
Beyond the Basics: Advanced Percentage Techniques
For more complex percentage problems involving multiple percentages or changes over time, you might need to utilize more advanced techniques such as:
-
Compound interest calculations: These calculations involve adding interest to the principal amount, and then calculating interest on the new total. This leads to exponential growth over time.
-
Percentage change calculations: Determining the percentage increase or decrease between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100%.
-
Using logarithms for exponential growth or decay: Logarithms are useful for solving problems involving exponential growth or decay, such as compound interest calculations with varying interest rates or population growth models.
Tips and Tricks for Efficient Percentage Calculation
-
Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can significantly speed up calculations.
-
Use a calculator effectively: Modern calculators can handle percentage calculations directly. Familiarize yourself with the percentage function on your calculator.
-
Practice regularly: The key to mastering percentage calculations is consistent practice. Work through various examples to build your confidence and speed.
Conclusion
Solving "28 is 40 percent of what number?" is a fundamental percentage problem, easily tackled using various methods. Understanding the underlying principles and practicing different approaches will enable you to confidently solve a wide range of percentage-related problems in various contexts, from everyday budgeting to complex financial calculations. By mastering these techniques, you can unlock a valuable skill applicable across numerous disciplines and improve your quantitative literacy. Remember to practice regularly to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
Equation Of Circle With Centre At Origin
May 12, 2025
-
How Many Protons Neutrons And Electrons Does Copper Have
May 12, 2025
-
Balanced Equation For The Combustion Of Hexane
May 12, 2025
-
Air Is An Element Compound Or Mixture
May 12, 2025
-
Which Is A Factor Of X2 8x 48
May 12, 2025
Related Post
Thank you for visiting our website which covers about 28 Is 40 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.