Which Is A Factor Of X2+8x-48
listenit
May 12, 2025 · 5 min read
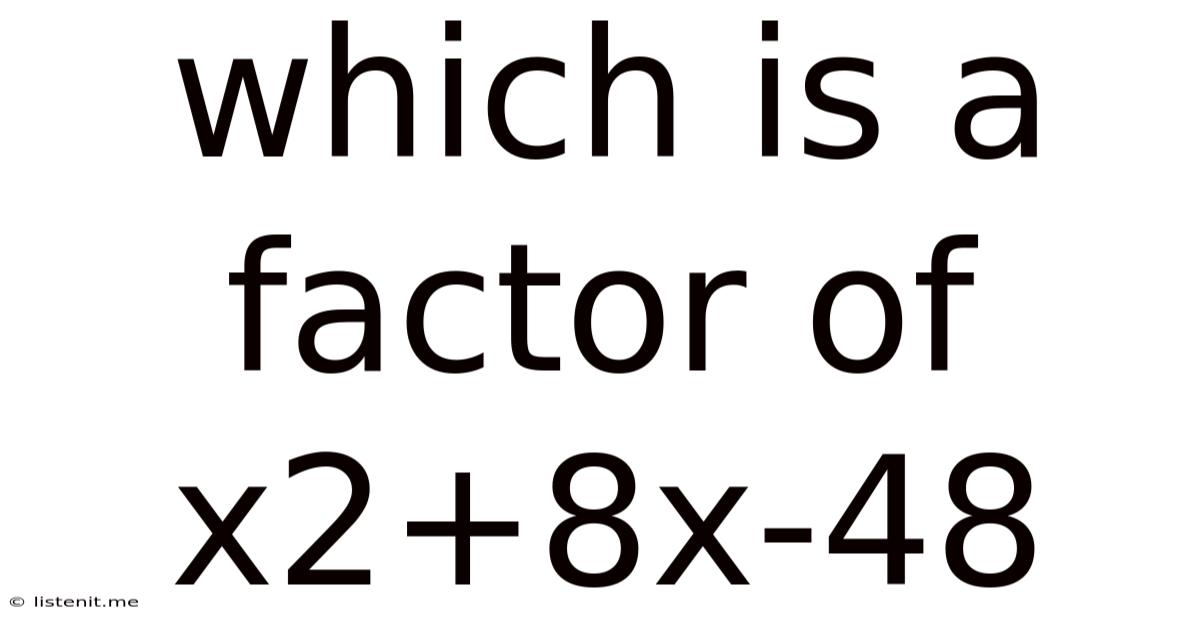
Table of Contents
Which is a Factor of x² + 8x - 48? A Comprehensive Guide to Factoring Quadratic Expressions
Finding the factors of a quadratic expression is a fundamental skill in algebra. Understanding how to factor these expressions opens doors to solving quadratic equations, graphing parabolas, and tackling more advanced mathematical concepts. This article delves deep into the process of factoring x² + 8x - 48, explaining the methods involved and providing a comprehensive understanding of the underlying principles. We'll explore multiple approaches, ensuring you grasp the concepts thoroughly and can confidently tackle similar problems in the future.
Understanding Quadratic Expressions
Before we dive into factoring x² + 8x - 48, let's briefly review the structure of a quadratic expression. A quadratic expression is an algebraic expression of the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, x² + 8x - 48, a = 1, b = 8, and c = -48.
The goal of factoring is to rewrite the quadratic expression as a product of two simpler expressions, typically two binomials. This factored form reveals the roots or zeros of the corresponding quadratic equation (ax² + bx + c = 0).
Method 1: Factoring by Finding Two Numbers
This is the most common method for factoring quadratic expressions where the coefficient of x² (a) is 1. We're looking for two numbers that:
- Add up to 'b' (the coefficient of x): In our case, b = 8.
- Multiply to 'c' (the constant term): In our case, c = -48.
Let's brainstorm pairs of numbers that multiply to -48:
- 1 and -48
- 2 and -24
- 3 and -16
- 4 and -12
- 6 and -8
- 8 and -6
- 12 and -4
- 16 and -3
- 24 and -2
- 48 and -1
Now, let's check which pair adds up to 8:
The pair 12 and -4 satisfies both conditions: 12 + (-4) = 8 and 12 * (-4) = -48.
Therefore, we can factor x² + 8x - 48 as (x + 12)(x - 4). This means that (x + 12) and (x - 4) are the factors of x² + 8x - 48.
Method 2: Using the Quadratic Formula
The quadratic formula is a powerful tool for finding the roots of any quadratic equation, even those that are difficult to factor using other methods. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, x² + 8x - 48, we have a = 1, b = 8, and c = -48. Substituting these values into the quadratic formula:
x = [-8 ± √(8² - 4 * 1 * -48)] / (2 * 1) x = [-8 ± √(64 + 192)] / 2 x = [-8 ± √256] / 2 x = [-8 ± 16] / 2
This gives us two solutions:
x₁ = (-8 + 16) / 2 = 4 x₂ = (-8 - 16) / 2 = -12
The roots are 4 and -12. Since (x - root) is a factor, we can write the factors as (x - 4) and (x + 12), confirming our result from Method 1.
Method 3: Completing the Square
Completing the square is another technique to solve quadratic equations and find factors. While less efficient for this particular problem, it's a valuable method to understand.
-
Move the constant term to the right side: x² + 8x = 48
-
Take half of the coefficient of x (8/2 = 4), square it (4² = 16), and add it to both sides: x² + 8x + 16 = 48 + 16
-
Factor the left side as a perfect square trinomial: (x + 4)² = 64
-
Take the square root of both sides: x + 4 = ±√64 = ±8
-
Solve for x: x = -4 + 8 = 4 x = -4 - 8 = -12
Again, we obtain the roots 4 and -12, leading to the factors (x - 4) and (x + 12).
Verifying the Factors through Expansion
To confirm our factorization, we can expand (x + 12)(x - 4) using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * -4 = -4x
- Inner: 12 * x = 12x
- Last: 12 * -4 = -48
Combining the terms, we get x² - 4x + 12x - 48 = x² + 8x - 48. This matches our original expression, confirming that (x + 12) and (x - 4) are indeed the correct factors.
Applications of Factoring Quadratic Expressions
The ability to factor quadratic expressions is crucial in various mathematical applications, including:
- Solving quadratic equations: Setting the factored expression equal to zero allows you to easily find the solutions (roots) of the equation.
- Graphing parabolas: The factors reveal the x-intercepts (where the parabola crosses the x-axis) of the quadratic function.
- Simplifying algebraic expressions: Factoring can simplify complex expressions, making them easier to manipulate and solve.
- Calculus: Factoring plays a vital role in calculus, particularly in finding derivatives and integrals.
- Physics and Engineering: Quadratic equations and their solutions are widely used in physics and engineering to model various phenomena, such as projectile motion and the behavior of electrical circuits.
Further Exploration: Factoring More Complex Quadratics
While this article focused on factoring a simple quadratic (where a = 1), the principles can be extended to more complex expressions where 'a' is not equal to 1. Methods like factoring by grouping or using the AC method become necessary in those cases. These techniques build upon the fundamental concepts explored here.
Conclusion
Factoring x² + 8x - 48 reveals the factors (x + 12) and (x - 4). This seemingly simple problem showcases the power of factorization in algebra and its wide-ranging applications in various fields. Mastering this skill provides a solid foundation for tackling more challenging algebraic problems and understanding deeper mathematical concepts. By understanding the different methods – finding two numbers, using the quadratic formula, and completing the square – you'll be well-equipped to handle a variety of quadratic expressions with confidence. Remember to practice regularly to solidify your understanding and develop your problem-solving skills.
Latest Posts
Latest Posts
-
What Gas Is Released During Photosynthesis
May 12, 2025
-
What Unit Is Used To Measure Air Pressure
May 12, 2025
-
What Affects The Rate Of Diffusion
May 12, 2025
-
How Do Elements Heavier Than Iron Form
May 12, 2025
-
Is The Square Root Of 5 Rational Or Irrational
May 12, 2025
Related Post
Thank you for visiting our website which covers about Which Is A Factor Of X2+8x-48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.