2 5 X 2 5 X 2 5
listenit
May 23, 2025 · 4 min read
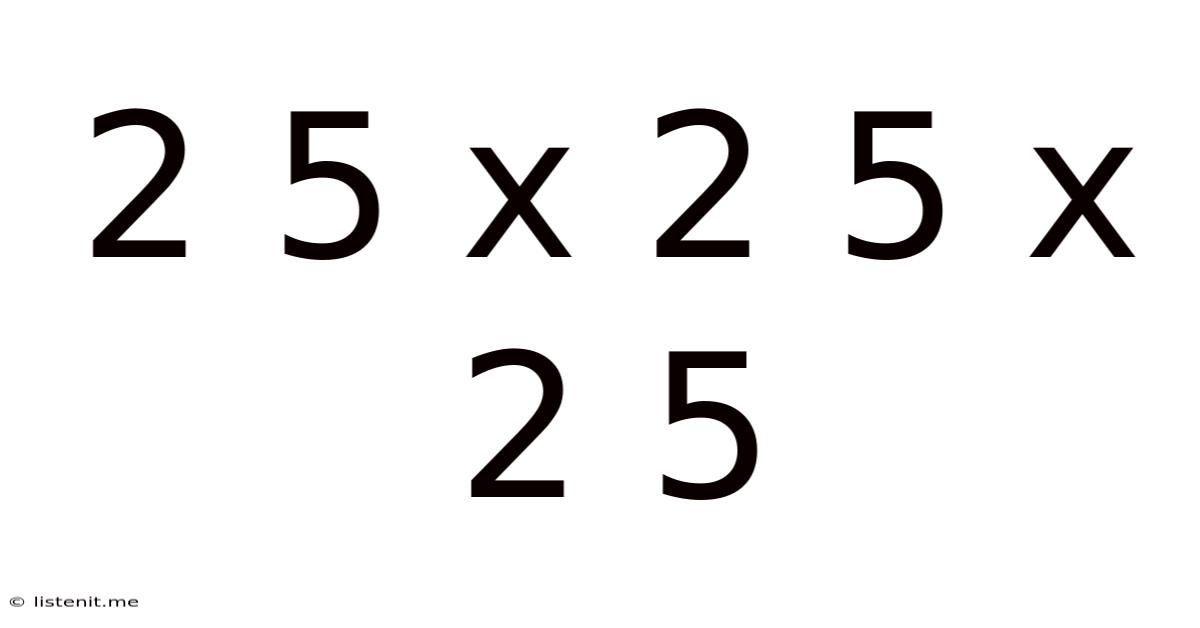
Table of Contents
Decoding 2.5 x 2.5 x 2.5: Exploring Volume, Cubes, and Practical Applications
The seemingly simple expression "2.5 x 2.5 x 2.5" might appear unremarkable at first glance. However, this seemingly straightforward calculation opens doors to a surprising array of concepts within mathematics, geometry, and even practical applications in various fields. This article delves deep into the meaning, implications, and real-world relevance of this cubic calculation, exploring its use in volume determination, cubic measurement systems, and its application in diverse scenarios.
Understanding the Fundamentals: Volume and Cubic Measurements
At its core, "2.5 x 2.5 x 2.5" represents a cubic calculation. It defines the volume of a cube with sides measuring 2.5 units each. Understanding the concept of volume is crucial. Volume is the amount of three-dimensional space occupied by an object or substance. It's measured in cubic units, which represent the amount of space contained within a cube with sides of a specific length. Common units for volume include cubic meters (m³), cubic centimeters (cm³), cubic feet (ft³), and cubic inches (in³).
The calculation 2.5 x 2.5 x 2.5 yields a volume of 15.625 cubic units. This means that a cube with sides of 2.5 units each occupies a space equivalent to 15.625 of those same cubic units. The importance of accurately calculating volume extends far beyond simple geometry exercises; it's fundamental to numerous engineering, construction, and scientific applications.
Beyond the Cube: Applications in Various Fields
The application of cubic calculations like 2.5 x 2.5 x 2.5 transcends theoretical mathematics. Let's explore some practical examples:
1. Construction and Engineering:
Imagine you're building a small, cubic storage unit with sides of 2.5 meters. Knowing the volume (15.625 cubic meters) is crucial for several reasons:
- Material estimation: Calculating the required materials, such as concrete, wood, or steel, directly depends on the volume. Accurate volume calculation prevents material waste and cost overruns.
- Structural design: The volume influences structural considerations. A larger volume might require additional support beams or reinforcement to ensure stability.
- Capacity planning: Knowing the volume helps determine the storage capacity of the unit, allowing for efficient space utilization.
2. Packaging and Shipping:
In logistics and shipping, understanding volume is paramount for efficient packaging and transportation. Consider a cubic package with sides of 2.5 feet. Calculating the volume (15.625 cubic feet) is essential for:
- Optimizing space: Knowing the volume helps determine how many packages can fit into a shipping container, maximizing space utilization and minimizing shipping costs.
- Weight and density calculations: Combined with weight information, volume helps calculate the density of the packaged goods, which is critical for determining freight charges and ensuring safe handling during transportation.
3. Liquid Measurement and Storage:
While not directly related to solid cubes, the principle of volume calculation extends to liquids as well. Imagine a cubic tank with sides of 2.5 meters designed to hold liquids. Knowing the volume (15.625 cubic meters) is essential for:
- Capacity determination: The volume defines the tank's capacity, indicating the maximum amount of liquid it can hold.
- Fluid dynamics: Understanding the volume is vital for calculations related to fluid flow, pressure, and other aspects of fluid mechanics.
4. Scientific Applications:
In scientific research, precise volume measurements are crucial. Consider experiments involving controlled environments or chemical reactions:
- Laboratory equipment: Many laboratory instruments, such as reaction vessels or storage containers, have specific volume capacities, often expressed in cubic centimeters or milliliters.
- Chemical reactions: Accurate volume measurements are essential for preparing solutions with precise concentrations, ensuring the reproducibility of experimental results.
Variations and Extensions: Beyond the Perfect Cube
While our primary focus is 2.5 x 2.5 x 2.5, which represents a perfect cube, the concept extends to other shapes and calculations:
- Rectangular Prisms: If the dimensions were not all equal (e.g., 2.5 x 3 x 4), the calculation would still yield the volume of a rectangular prism, a three-dimensional shape with rectangular sides.
- Irregular Shapes: Calculating the volume of irregular shapes requires more advanced techniques, such as water displacement or numerical integration. However, the fundamental principle of volume remains consistent.
Practical Tips and Considerations
- Unit Consistency: Always ensure consistency in units when calculating volume. Mixing units (e.g., meters and centimeters) will lead to incorrect results.
- Significant Figures: Pay attention to significant figures in measurements to avoid unnecessary precision or rounding errors in calculations.
- Real-World Limitations: Remember that real-world objects rarely have perfectly defined dimensions. Slight variations in measurements can affect the calculated volume.
Conclusion: The Significance of Simple Calculations
The seemingly simple calculation of 2.5 x 2.5 x 2.5 reveals the fundamental importance of understanding volume and cubic measurements. Its applications extend far beyond theoretical exercises, playing a critical role in various fields, from construction and engineering to packaging and scientific research. Mastering these basic calculations builds a solid foundation for tackling more complex problems in geometry, mathematics, and real-world applications. By understanding volume calculations, we gain a deeper appreciation of the three-dimensional world around us and the mathematical tools used to quantify and interpret it. The simplicity of 2.5 x 2.5 x 2.5 belies its profound implications in numerous practical scenarios.
Latest Posts
Latest Posts
-
What Is 1 3 Plus 1 3 In Fraction Form
May 23, 2025
-
What Time Is 34 Hours From Now
May 23, 2025
-
0 5 Is What Percent Of 20
May 23, 2025
-
What Is Half Of 23 And 5 8
May 23, 2025
-
3 4 Divided By 1 8 In Fraction
May 23, 2025
Related Post
Thank you for visiting our website which covers about 2 5 X 2 5 X 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.