3/4 Divided By 1/8 In Fraction
listenit
May 23, 2025 · 5 min read
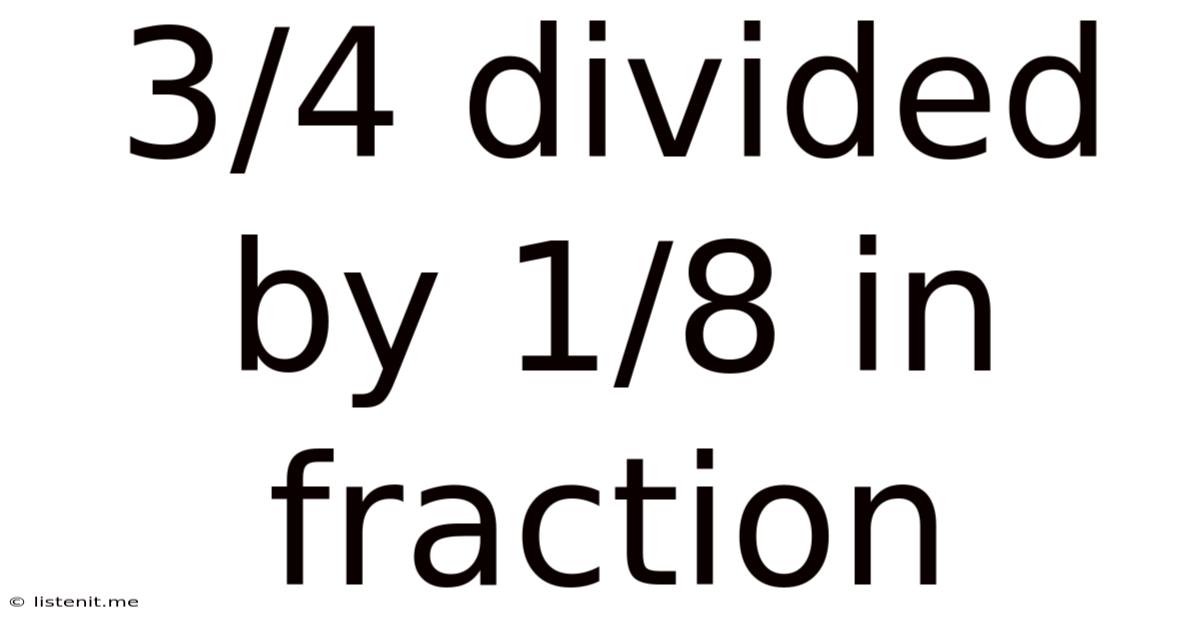
Table of Contents
3/4 Divided by 1/8: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes second nature. This comprehensive guide will walk you through the division of 3/4 by 1/8, explaining the underlying principles and providing various approaches to solve the problem. We'll also explore the practical applications of fraction division and offer tips for mastering this essential mathematical skill.
Understanding Fraction Division
Before diving into the specific problem of 3/4 divided by 1/8, let's establish a solid foundation in fraction division. The core concept revolves around the idea of reciprocals and multiplication.
Instead of directly dividing by a fraction, we transform the division problem into a multiplication problem. This is achieved by multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/8 is 8/1 (or simply 8).
Therefore, the rule for dividing fractions is: Keep the first fraction the same, change the division sign to a multiplication sign, and flip (find the reciprocal of) the second fraction.
Solving 3/4 Divided by 1/8
Now, let's apply this rule to our problem: 3/4 divided by 1/8.
-
Keep the first fraction: We keep 3/4 as it is.
-
Change the division sign to multiplication: The division sign (÷) becomes a multiplication sign (×).
-
Flip the second fraction: The reciprocal of 1/8 is 8/1.
Our problem now transforms from:
3/4 ÷ 1/8
to:
3/4 × 8/1
-
Multiply the numerators and the denominators:
- Multiply the numerators: 3 × 8 = 24
- Multiply the denominators: 4 × 1 = 4
This gives us the fraction 24/4.
-
Simplify the fraction: We can simplify 24/4 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 4.
24 ÷ 4 = 6 4 ÷ 4 = 1
Therefore, the simplified answer is 6/1, which is equivalent to 6.
So, 3/4 divided by 1/8 equals 6.
Alternative Methods for Solving Fraction Division Problems
While the method described above is the standard approach, there are other ways to tackle fraction division problems. Let's explore a couple of them:
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions before dividing. This approach can be helpful for visualizing the problem, especially for beginners.
-
Find a common denominator: The least common multiple (LCM) of 4 and 8 is 8.
-
Convert fractions to equivalent fractions with the common denominator:
- 3/4 is equivalent to 6/8 (multiply both numerator and denominator by 2)
- 1/8 remains as 1/8
-
Divide the numerators: Now we divide the numerators: 6 ÷ 1 = 6
-
Keep the common denominator: The denominator remains the same, so the result is 6/1, which simplifies to 6.
This method demonstrates the division conceptually, showing how many times 1/8 fits into 6/8.
Method 3: Visual Representation with Fraction Circles or Bars
A visual approach can be particularly beneficial for understanding fraction division. Using fraction circles or bars, you can represent 3/4 and 1/8 visually. Then, you can physically see how many times 1/8 fits into 3/4, leading to the answer of 6. While this method is less efficient for complex problems, it's excellent for building intuitive understanding.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous real-world applications. Consider the following examples:
-
Cooking and Baking: Recipes often require dividing ingredients. For example, if a recipe calls for 3/4 cup of flour and you want to halve the recipe, you'd need to divide 3/4 by 2 (or 2/1), resulting in 3/8 cup of flour.
-
Sewing and Crafting: Cutting fabric or other materials accurately often involves fractional measurements and divisions.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering often involve fractions and the need for division.
-
Data Analysis: Many data analysis tasks involve working with fractions and proportions, often requiring division.
-
Financial Calculations: Calculating shares of profits or splitting costs involves dividing fractions.
These examples highlight the practical relevance of understanding and mastering fraction division.
Mastering Fraction Division: Tips and Practice
Becoming proficient in fraction division requires consistent practice and a solid grasp of the fundamental concepts. Here are some tips to help you master this skill:
-
Practice Regularly: The more you practice, the more confident and efficient you'll become. Start with simple problems and gradually increase the complexity.
-
Understand the Concepts: Don't just memorize the steps; understand why the method works. This will make problem-solving easier and more intuitive.
-
Use Visual Aids: Visual aids like fraction circles or diagrams can be invaluable for understanding the process, especially in the beginning stages.
-
Check Your Answers: Always double-check your answers to ensure accuracy. You can do this by multiplying your answer by the divisor to see if you get the dividend.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable steps.
-
Seek Help When Needed: Don't hesitate to ask for help if you're struggling. A tutor, teacher, or online resource can provide valuable support.
Conclusion: Embrace the Power of Fraction Division
Fraction division, while initially appearing challenging, is a fundamental skill with broad applications. By understanding the principles of reciprocals, mastering the standard algorithm, and exploring alternative methods, you can confidently tackle any fraction division problem. Regular practice and a focus on conceptual understanding will solidify your skills and unlock the power of this essential mathematical operation. Remember, with consistent effort and the right approach, mastering fraction division is entirely achievable. So, embrace the challenge, practice regularly, and watch your skills flourish!
Latest Posts
Latest Posts
-
What Is 5 Divided By 5
May 24, 2025
-
How Fast Is 8 Miles A Minute
May 24, 2025
-
25 Is What Percentage Of 100
May 24, 2025
-
If You Are Born In 1980 How Old Are You
May 24, 2025
-
What Percent Is 6 Of 16
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 1/8 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.